Using Cooperative Learning in a Large Introductory Statistics Class
Rhonda C. Magel
North Dakota State University
Journal of Statistics Education v.6, n.3 (1998)
Copyright (c) 1998 by Rhonda C. Magel, all rights reserved. This text may be freely
shared among individuals, but it may not be republished in any medium without express
written consent from the author and advance notification of the editor.
Key Words: Examples of exercises; Team selection.
Abstract
This article discusses one active learning technique, cooperative learning, that can be
used in large classes. This technique requires that students be divided into learning
teams. A method for quickly dividing a large class of students into learning teams is
presented. Two examples of cooperative learning exercises used in an introductory
statistics class are given. These serve as illustrations of the type of cooperative
learning exercises that can be assigned in a large class. In particular, these exercises
were used in a class of 195 students. Preliminary findings by the instructor of the
advantages of using cooperative learning exercises are discussed.
1. Introduction
1 Research has indicated that students have different learning styles and that their
academic performance is related to their learning style and the method of teaching used.
If the method of teaching used coheres with their learning style, students tend to do well
academically. If the teaching method does not fit their learning style, students tend not
to do as well (Higbee, Ginter, and Taylor 1991). Because of the
different learning styles of students, faculty are encouraged to use different teaching
techniques in their classrooms. One such technique is cooperative learning. Cooperative
learning is a form of active learning in which small groups work together on exercises
designed to improve learning. As instructors try cooperative learning, however, they
frequently run into problems of execution. Many of these problems involve management of
the cooperative learning process. This paper discusses one way to overcome a common
management problem associated with cooperative learning.
2 Most instructors of large classes resort to the standard lecture format. Studies have
indicated that the lecture occupies 80% to 95% of the class time in these classes (Benjamin 1991). The aural-oriented and perhaps print-oriented
learner will do well in this type of format, but a student with one of the other learning
styles probably will not do as well at processing and retaining the information (Higbee et al. 1991).
3 Benjamin (1991) believes that instructors of large classes
often resort to a lecture format because it is easier, and it is safer. There is less that
can go wrong when doing a lecture. However, he encourages instructors of these classes to
try some active learning techniques.
4 I will start by examining cooperative learning a little more closely. Cooper, McKinney, and Robinson (1991) define cooperative learning as
"a structured, systematic instruction strategy in which small groups work together
for a common goal" (p. 239). Cooper and Mueck (1990) define
six critical features of cooperative learning.
- Everyone on a learning team is responsible for the other team members' learning.
- Cooperative learning exercises are intended for learning, not for significantly
affecting students' grades. Projects done in teams are given little weight. They are
thought of as learning experiences. Most of a student's grade comes from individual
assignments or tests.
- There should be an appropriate assignment of students to teams.
- The teacher now serves as a facilitator rather than as an expert dispensing knowledge.
- Attention is given to social skills since students must learn to cooperate with each
other.
- Students gain experience in verbal problem solving.
5 Studies at the K-12 level on cooperative learning indicate many positive advantages
over teaching using a more traditional method (Johnson, Maruyama,
Johnson, Nelson, and Skon 1981; Slavin 1983). The preliminary
results of Cooper and Mueck (1990) on the effects of cooperative
learning at the collegiate level also indicate positive findings.
2. Using Cooperative Learning
6 At North Dakota State University we teach several sections per year of an
introductory statistics class with the sections ranging in size from 150 to 210. The class
is worth three credits and is designed to cover the following material:
- An introduction to statistics
- Graphing and displaying data
- Measures of location and
variability
- Probability and random variables
- Binomial random variables
- Normal probabilities
- Central limit theorem
- Estimation (eight different
confidence intervals are introduced)
- Hypothesis testing (eleven different
hypothesis tests are introduced including the chi-square goodness-of-fit test and
chi-square test of independence).
7 Because the class is a prerequisite to other classes on campus, instructors are not
given the option of omitting any topics. Most of the students taking this class are in
their junior year. Their major areas vary, including business, child development,
psychology, agriculture, sociology, biochemistry, zoology, and food and nutrition.
8 Students taking the introductory statistics class attend a large lecture portion
twice a week, meeting 50 minutes each time. All of the students in a particular section of
this class meet in the large lecture. One section is split into five smaller ones once a
week for students to attend computer labs and/or take quizzes. A faculty member teaches
the large lecture portion for a section of this class. Graduate teaching assistants
conduct the computer labs and/or monitor short quizzes. Exams are given in the large
lecture portion. All of the comments that follow refer to activities in the large lecture
portion.
9 I have taught many sections of this introductory statistics class during the time I
have spent at North Dakota State University. During one spring semester, I had a section
of this class consisting of 195 students. It was during this spring that I decided to
experiment with using cooperative learning.
10 Prior to this time, I had been using an active learning technique in my classroom.
Approximately 25 minutes of every large lecture portion class was spent lecturing. For the
remainder of the class, every student was given a worksheet to complete. The worksheet was
to be turned in at the end of the class period. Students could work alone or with other
students of their choosing, but each student needed to complete his or her own worksheet.
Some of the worksheets used are given in Magel (1996).
11 When using this active learning technique, I was originally concerned about whether
I could cover all the material that I had covered when I had used a standard lecture
format. It turned out this was not a problem. Everything did end up getting covered. The
average exam scores of the students also, if anything, improved. Further details are given
in Magel (1996).
12 Overall, I was fairly happy with this technique, but I had noted at times students
who had poor quantitative reasoning skills would work with other students of the same
type. I spent some time helping these groups, but they were not benefiting as fully from
the classroom experience as I felt they would if they worked with students with more
highly developed quantitative reasoning skills.
13 It is because of this observation that I decided to experiment with using
cooperative learning in the class. One problem that I initially faced in doing this was
how to quickly divide the students into learning teams. I felt that it would be best to
randomly assign students to teams since I did not know the personalities and abilities of
the students well enough (there were 195 of them) to figure out which students would work
well together. I also wanted to vary the teams each time, and I needed a quick way to do
it.
14 The class that I was teaching was given in a standard auditorium consisting of three
sections (left, middle, and right). After examining the layout of the auditorium, I
decided to have learning teams assemble in 13 rows of each section. Rectangles were cut
from 13 different colors of construction paper and marked with one of the numbers
"1", "2", and "3" ahead of time. The number on each card
represented a section of the auditorium with "1" = left, "2" = middle,
and "3" = right. The color represented a row in that section. Five cards of each
combination were made. This was the maximum size of each team.
15 The cards were shuffled and given to the students as they came into the classroom on
the day that a cooperative learning exercise was to be used. It should actually be noted
that the auditorium I was using had three different doors, and so I had to do the best
that I could at passing out cards. I made sure that every student did have a card before
we started. Students originally sat wherever they wanted to until it was explained what we
were going to do in class that day, and how we were going to split up into groups.
Students were then to go to the section designated by the number on their cards and then
to the row of that section designated by the color they were holding. The colors that were
to represent the rows were placed on an overhead transparency so that students could
determine which row corresponded to their color. For example, students holding blue cards
would go to the first row of their assigned section. Students holding tan cards would go
to the second row, purple cards to the third row, and so on.
16 The first time that I used this method for dividing students into teams, it took
approximately two to three minutes for everyone to get to their appropriate places.
Different teams were formed by the same method the next time I used a cooperative learning
exercise. The process of dividing students into teams took less than two minutes the
second time.
17 Not every auditorium will be in exactly the same arrangement as the one I was using.
For example, I have been in some auditoriums with one large section and one small section.
In this case, the large section could possibly be divided in half by using a seat number.
The instructor will have to adapt the above technique to fit his or her classroom
conditions. The point here is that we can take an auditorium designed for lecturing and
use it to do small group cooperative activities.
18 Two examples of cooperative learning exercises that I gave in my class follow. The
first exercise (Example 1) was given on Valentine's Day. It was an effort to get the
students to understand and reinforce the concept of a discrete random variable, its
probability distribution, and the mean and variance of a random variable. It was also
given to further reinforce the idea of sampling with replacement versus sampling without
replacement.
19 Each learning team was given an envelope containing a mixture of red, white, and
pink M&M's. Students were then required to work on the following sheet (Example 1).
They could get help from other team members. Teams could also ask questions of me. Members
of the team were required to check and discuss answers with each other before turning in
the worksheet. No member was to turn in his or her worksheet until all members were done.
One downfall of this process is that it is hard to monitor in a large class to what extent
the first critical feature of cooperative learning, namely everyone on a learning team is
responsible for the other team members' learning, is met. This was certainly encouraged by
telling students that answers should be discussed and checked with other team members, and
by not allowing students to turn in worksheets early. I also required each student to list
the names of the other team members on their sheet.
20 Many teams had questions getting started with this exercise. I gave all the teams a
hint after letting students think about this for a few minutes. This was done to keep the
process moving. I am pointing out this particular part because it is the instructor's job
in Cooperative Learning to serve as the facilitator. If problems arise in doing the
exercise, adjustments must be made. At the end of the 50-minute class period,
approximately half of the teams had completed the exercise. The other half asked to take
it home to complete it, and to bring it back the next time. This exercise was not to be
graded for accuracy and every student who made a reasonable attempt to complete it was
awarded five points (even if they didn't complete it since we were under a time
constraint). It was a good sign that students wanted to complete it.
21 No lecture or examples were given during this class period. Random variables,
probability distributions, and the mean and variance of a random variable had been defined
earlier. Instead of doing additional examples in class, I let students work on their own.
This goes along with Cobb's (1991) proposal that we as instructors
should do less lecturing.
EXAMPLE 1:
STAT 330
NAME: ______________________________
Worksheet
Happy Valentine's Day1. Count the number of M&M's in the envelope.
Number of Pink = ____
Number of Red = ____
Number of White = ____
Suppose three M&M's are randomly drawn from the envelope one at a time and without
replacement.
(a) Write down the sample space.
(b) Let X = the number of pink M&M's drawn. What values could X assume?
(c) Find the probability function for X.
(d) Find the E(X). Write a brief interpretation of this value.
(e) Find the standard deviation of X.
(f) Graph the probability histogram of X.
(g) Check and discuss answers with other team members before going on to Number 2.
2. Suppose now that a random sample of size three is drawn with replacement. Let
X = the number of pink M&M's drawn.
(a) Find the probability function of X.
(b) Find E(X) and the standard deviation of X.
(c) Graph the probability histogram of X.
(d) Check and discuss answers with other team members. |
22 A second example of a cooperative learning exercise (Example 2) was given to help
students understand the concept of estimating the difference between two population
proportions. Students had been given the formula for the confidence interval for p1 -
p2, but examples had not been worked. Each team was given two sets of cards. The first
set of cards was to represent a population of people given treatment A to fight a
particular type of cancer. The students were to estimate the proportion of people from
this population who survived at least five years after receiving treatment A, p1. Each
card had either a "0" or a "1" on it with "0" indicating
that the person died before the end of the five years, and a "1" indicating that
the person selected had survived at least five years.
EXAMPLE 2:
STAT 330
NAME: ___________________________
DATE: ___________________________
In-Class
1. Assume the cards you are given represent a population of people given treatment A to
fight a particular type of cancer. This population is very large. We want to estimate the
proportion of people who survived at least five years, p1. We will do this by randomly
drawing a sample of size 20 from this population. Shuffle the cards, draw 1 card, replace
it, shuffle the cards, draw another card, replace it, etc. A "1" indicates that
the person selected has survived at least five years. A "0" indicates that the
person selected has died before the end of the five years.
A point estimate for p1 is:
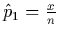 , ,
where in this case x is the number of people in the sample who survived at least five
years.
(a) Write down your point estimate of p1.
(b) Find a 90% confidence interval for p1.
(c) Examine your cards. What is the true value of p1?
(d) Is the value of p1 in your confidence interval?
(e) Discuss results with members of your team.
2. The second deck of cards you received represents a population of people given treatment
B to fight the same type of cancer. Randomly draw a sample of size 20 from this population
and estimate the proportion of people receiving treatment B who survive at least five
years, p2.
(a) Write down your point estimate of p2.
(b) Write down your point estimate of p1 - p2.
(c) Find a 90% confidence interval for p1 - p2.
(d) Examine your confidence interval for p1 - p2. Can you conclude one treatment is
better than the other? Why or why not?
(e) Look at your second set of cards and write down the true value of p1 - p2.
(f) Is the true value of p1 - p2 in your confidence interval?
(g) Discuss results with members of your team. |
23 Students were to randomly select twenty cards, one at a time, always replacing the
card they drew and reshuffling the cards before making the next draw. One team member was
responsible for holding and reshuffling the cards. All other team members were to be given
an opportunity to draw cards. The cards were to represent a very large population and thus
the probability of drawing a "1" always remained the same.
24 After calculating a point estimate and a 90% confidence interval for p1, the
students were to examine their cards and write down the true value of p1. Each group had
10 total cards. If a "1" appeared on three of them, their cards represented a
population in which p1 = 3/10 = 0.3. This value varied from team to team. The students
were then asked whether the value of p1 was in their confidence interval. This exercise
was an attempt to get students to understand the concept of estimation. Members of each
team were supposed to check their answers with each other before proceeding to the next
part. This was done in order to try and meet the first critical feature of cooperative
learning, that everyone on a learning team is responsible for the other team members'
learning. As stated earlier, this feature of cooperative learning is hard to monitor in
this setting. The best that I felt I could do was to try to encourage it.
25 The second set of cards each team was given was to represent a population of people
given treatment B to fight the same type of cancer. Students were to draw a random sample
of size 20 as before. They were then to use their estimate of p2, and of p1 in the first
part, to derive a 90% confidence interval for p1 - p2. Next, they were to look at their
cards and find the true value of p2, then of p1 - p2, and determine if the value of p1
- p2 was in their confidence interval. This was again to get students to understand what
p1 - p2 measured and the idea of estimating this quantity by a confidence interval.
Student teams were again supposed to discuss and check their answers.
26 It should be noted that throughout the semester, I interspersed cooperative learning
exercises with the active learning technique that I had been using earlier. That is, I
continued at times to let students do worksheets either by themselves or with one or two
other students. The exercises on these worksheets did not require one to interact with
other students in order to complete them. I used both techniques in this class, because
some students felt more comfortable choosing the students that they wanted to work with
(or in some cases alone), but at times I wanted to mix students up and force them to
interact with other students. I wanted to make sure that the weaker students participated
in some interactions and did not always work with other weaker students.
3. Results
27 Three exams are given in my class during the course of one semester. Eighty percent
of a student's grade comes from these exams. The cooperative learning exercises that
students did this spring semester were based on material covered on the first and third
exams. For each of those exams, the cooperative learning exercises used more than half the
concepts covered. After the class was over for this spring, I decided to go back and
compare the students' performance in this class with the students' performance in the
class that I had taught during the previous spring semester. I thought it would be better
to use the previous spring semester's class (rather than fall, as originally planned) to
keep the students as homogeneous as possible. Some departments encourage their student
majors to take this class during a particular semester (spring or fall).
28 The three exams given in both classes were not the same, although they did cover the
same material, and I tried to make them of the same level of difficulty. It would be
virtually impossible to keep the three exams exactly the same and have any meaningful
interpretation of the comparisons of the two sets of scores, because students in the
earlier class would give information to students in the later class. Preliminary findings
indicated that, on average, students' scores improved when cooperative learning exercises
were used. I would hesitate, however, to use these findings to say that more learning had
taken place. These tests were not standardized.
29 Exam Number 1 covers topics 1 through 4 as mentioned earlier. In the class in which
cooperative learning exercises were not used, 8.28% of the students' scores on this exam
were below 60, and 8.92% of the scores were in the 60's. When cooperative learning
exercises were used, only 2.03% of the students' scores were below 60, and 5.08% were in
the 60's. This gives some indication that weaker students may benefit. Similarly, on Exam
Number 3, there was a lower percentage of scores below 70 when cooperative learning
exercises were used. This exam covers topics 8 and 9 as mentioned earlier. When
cooperative learning exercises were not used, 28.76% of the students scored below 60, and
18.95% scored in the 60's. This changed to 20% scoring below 60 and 13.51% scoring in the
60's when the exercises were used.
30 Some students indicated on evaluation forms at the end of the semester that they
liked doing the cooperative learning exercises. Other students commented that they would
rather choose their own teams.
31 The students in the class appeared to be actively involved in doing both of the
cooperative learning exercises mentioned in this paper. Every group had extensive
discussion during the exercises. Students' discussions in class were on the exercise. In
some teams, members were debating which of two methods was the correct way to solve the
problem. I did get asked after awhile which way was correct. In other teams, a member was
explaining to another member how to go about solving a particular problem.
4. Conclusions
32 Cooperative learning exercises can be used in a large class, at least one of size
195. They do require planning ahead of time. Dietz (1993), who used a
cooperative learning exercise to teach sampling in a statistics class of size 41, has also
pointed out that planning is crucial. The instructor must be willing to try something
different, not worry that something may go wrong, and be ready to make adjustments to the
exercise in class. The instructor may have to experiment with different ideas and find out
what works best for his or her situation.
33 It has been my experience that a majority of the students enjoyed doing cooperative
learning activities (or perhaps just having a variety of different activities). Some
students did indicate they would have preferred to select their own teams. Dietz's (1993) findings also support this. However, in order to achieve
my purpose of not having some of the students with weaker quantitative reasoning skills
working with students of the same type, I needed to be the one who assigned teams. What I
felt was a good compromise was doing approximately four cooperative learning exercises in
class for which there were randomly assigned teams, and also continuing with the other
active learning technique which allowed students to work alone or with other students of
their choosing.
34 The random method of assigning students to teams might not always give the best team
formations. Weaker students could still end up with weaker students, but it was the best I
could hope for since it would be hard to know all of the students' abilities. I also
randomly assigned students to new teams each time a cooperative learning exercise was to
be done. If a student was on a team that did not work well together the first time, the
student would at least have a chance of being on a team that worked well together for the
next exercise.
35 Preliminary findings based on comparing exam scores from this spring semester's
class with the class from the previous spring semester indicate that there was a
significant increase on the average exam score when cooperative learning exercises were
used. A smaller percentage of students also scored below 70. There were too many other
factors involved to claim that cooperative learning exercises were responsible for this,
but these findings merit further investigation.
36 I do think that what is important is to give students a variety of experiences in
class. This keeps things interesting and should help make learning statistics fun!
References
Benjamin, L. T., Jr. (1991), "Personalization of Active
Learning in the Large Introductory Psychology Class," Teaching of Psychology,
18(2), 68-74.
Cobb, G. (1991), "Teaching Statistics: More Data, Less
Lecturing," UME Trends, 3.
Cooper, J., and Mueck, R. (1990), "Student Involvement in
Learning: Cooperative Learning and College Instruction," Journal on Excellence
in College Teaching, 1, 68-76.
Cooper, J., McKinney, M., and Robinson, P. (1991),
"Cooperative/Collaborative Learning: Part II," The Journal of Staff,
Program and Organizational Development, 9(4), 239-52.
Dietz, E. J. (1993), "A Cooperative Learning Activity on
Methods of Selecting a Sample," The American Statistician, 47, 104-108.
Johnson, D. W., Maruyama, G., Johnson, R. T., Nelson, D., and Skon,
L. (1981), "Effect of Cooperative, Competitive, and Individualistic Goal
Structures on Achievement: A Meta-Analysis," Psychological Bulletin, 89, 47-62.
Higbee, J. L., Ginter, E. J., and Taylor, W. D. (1991),
"Enhancing Academic Performance: Seven Perceptual Styles of Learning," Research
Teaching in Developmental Education, 7(2), 5-10.
Magel, R. C. (1996), "Increasing Student Participation in
Large Introductory Statistics Classes," The American Statistician, 50, 51-56.
Slavin, R. E. (1983), "When Does Cooperative Learning
Increase Student Achievement?," Psychological Bulletin, 94, 429-445.
Rhonda C. Magel
Department of Statistics
North Dakota State University
Fargo, ND 58105
magel@prairie.nodak.edu
Return to Table of Contents |
Return to the JSE Home Page
![]() ,
,