K. L. Weldon
Simon Fraser University
Journal of Statistics Education v.8, n.3 (2000)
Copyright (c) 2000 by K. L. Weldon, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the author and advance notification of the editor.
Key Words: Distance; Prediction error; Root mean square; Standard deviation; Standardized variables.
The simplest forms of regression and correlation involve formulas that are incomprehensible to many beginning students. The application of these techniques is also often misunderstood. The simplest and most useful description of the techniques involves the use of standardized variables, the root mean square operation, and certain distance measures between points and lines. On the standardized scale, the simple linear regression coefficient equals the correlation coefficient, and the distinction between fitting a line to points and choosing a line for prediction is made transparent. The typical size of prediction errors is estimated in a natural way by summarizing the actual prediction errors incurred in the dataset by use of the regression line for prediction. The connection between correlation and distance is simplified. Despite their intuitive appeal, few textbooks make use of these simplifications in introducing correlation and regression.
1 The introduction to association between two quantitative variables usually involves a discussion of correlation and regression. Some of the complexity of the usual formulas disappears when these techniques are described in terms of standardized versions of the variables. This simplified approach also leads to a more intuitive understanding of correlation and regression. More specifically, the following facts about correlation and regression can be simply expressed.
2 The correlation r can be defined simply in terms
of standardized variables zx and
zy as ![]() zxzy /n.
zxzy /n.![]() . Correlation is related to the
perpendicular distances from the standardized points to the
line of slope 1 or -1, depending on the sign of the
correlation. In fact, the root mean square of these
perpendicular distances is
. Correlation is related to the
perpendicular distances from the standardized points to the
line of slope 1 or -1, depending on the sign of the
correlation. In fact, the root mean square of these
perpendicular distances is ![]() .
.
3 The key to these simplifications and interpretations is an understanding of the standardization process. For this it is necessary for students to understand that a standard deviation really does measure typical deviations. This is aided by the use of the "n" definition of the standard deviation:
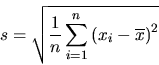
It is apparent that this is the average squared
deviation, and taking the square root of this is a natural
step to recover the original units. So a standardized
observation ![]() is the number of these
"typical" deviations that an observation is from the mean.
This describes the measurement relative to the (sample)
distribution from which it comes.
is the number of these
"typical" deviations that an observation is from the mean.
This describes the measurement relative to the (sample)
distribution from which it comes.
4 For students who must deal with traditional courses and textbooks using a strictly formula-based approach, it may be necessary to use the suggestions here in a first introduction. Once this simple introduction is accomplished, the more traditional approach could still be used, and shown to yield essentially the same results. The simplified introduction gives an easy-to-absorb sense of the strategy, and statistical software can take care of the slightly different arithmetic that working with standardized variables entails. The simplified approach suggested here has been used in many semesters of an introductory course based on the text by Weldon (1986), and no n vs. n - 1 confusion has been noted by the students or by instructors of subsequent statistics courses.
5 The definition r = ![]() zxzy /n
assumes that the "n" definition of the standard
deviation is used. A similar definition using the
"n - 1" definition of the standard deviation would
require the n in the denominator to be replaced by
zxzy /n
assumes that the "n" definition of the standard
deviation is used. A similar definition using the
"n - 1" definition of the standard deviation would
require the n in the denominator to be replaced by
6 It is important for students to realize that the
regression line is not a simple curve fit to the points,
but rather a line designed for prediction. The formula
7 Regression predictions can be made with the regression
equation expressed in original units, but the direct use of
![]() , and can
then be transformed back to original units.
, and can
then be transformed back to original units.
8 It is well known that stretching one scale of a scatterplot can increase the apparent correlation (even though the correlation is actually unchanged). Portraying data in their standardized scale removes this illusion. It also makes the point that the correlation does not depend on the scales of the variables. Moreover, "banking to 45o" (that is, choosing an aspect ratio for the plot that portrays trends as close to ± 45o as possible) is recommended for graphical assessment (Cleveland 1993).
9 The distance of a point (x0,
y0) to a line ![]() . Expanding and
using
. Expanding and
using ![]() produces the well-known result that the root mean square
distance of the data from the regression line is
produces the well-known result that the root mean square
distance of the data from the regression line is ![]() times the
standard deviation, which in this case is 1. The condition
times the
standard deviation, which in this case is 1. The condition
![]() only depends on the use of the "n" definition for
the standard deviation—with the "n - 1"
definition of r and the standard deviation, the same
result is true.
only depends on the use of the "n" definition for
the standard deviation—with the "n - 1"
definition of r and the standard deviation, the same
result is true.
10 The minimum (i.e., orthogonal) distance of a point
(x0, y0) to a line
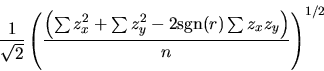 = = |
(1) |
This result appeared in Weldon (1986).
11 This "n" definition simplifies many things in
teaching statistics. The justification for the more common
![]() , which is not
really relevant for estimation of
, which is not
really relevant for estimation of ![]() . One could even
question the need for unbiasedness when it costs us in
terms of mean squared error. The "n" definition is
easier to explain and has smaller mean squared error.
. One could even
question the need for unbiasedness when it costs us in
terms of mean squared error. The "n" definition is
easier to explain and has smaller mean squared error.
12 Some instructors are reluctant to use the "n" definition of the sample standard deviation because it complicates the discussion of the t-statistic. But actually, if the t-statistic is defined in terms of the "n" definition of the sample standard deviation, the divisor "n - 1" appears in its proper place as a degrees-of-freedom factor, preparing the student in a natural way for the chi-square and F-statistics:
The s in this formula is
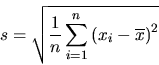
as before. Nevertheless, for instructors who wish to stick with the "n - 1" definition, the approach to correlation and regression given in the rest of this paper will still hold together.
13 Another reason for avoiding the n definition is the confusion that might be caused by the majority preference for the n - 1 definition in other textbooks. However, once the idea of standard deviation is understood through the simplest approach, the existence of variations may not be so disturbing. The n - 1 definition can be viewed in regression contexts as an "improvement" on the n definition, and its extensions to the multi-parameter case will likely be accepted without too much consternation.
14 To illustrate the above formulas, consider the following dataset relating performance on a mathematics test with performance on a verbal test. The data were sampled from a larger dataset in Minitab (1994). The first step for the student is to plot the data. Using the default scaling, Minitab produces the plot in Figure 1.
Figure 1. Scatterplot of "Grades" Data from Minitab. The scaling is the default scaling used by Minitab.
15 If the variables are centered, and the scales
equalized, we obtain the plot in Figure 2.
On this scale, it can be seen that the perpendicular distances of the
points from the line of slope one (which may be called the
point-fit line or the SD line) are usually less than one
but greater than 0.5. Equation (1)
says that the root mean square of these distances is equal
to ![]() . In this case, the sample correlation
r is approximately 0.5, so the root mean square
distance is 0.7, which is about what we expect from
visualizing the graph.
. In this case, the sample correlation
r is approximately 0.5, so the root mean square
distance is 0.7, which is about what we expect from
visualizing the graph.
Figure 2. Equal-Scales Scatterplot of "Grades" Data. Both scales are in standardized units.
16 Another observation that can be made from the graph concerns the average product. The average product is the correlation, and the idea of this can be gleaned from a graph like Figure 3, in which the points are annotated with the product of the standard scores. The fact that the average product is 0.5 is not obvious, but one can at least see which quadrants must have the largest contributions to the average in order that the correlation be positive.
Figure 3. Pointwise Contributions to the Correlation Coefficient. The average of these zxzy contributions is the correlation coefficient.
17 Another feature of the "average product" definition of the correlation is the ability to detect outliers. From the graph it can be observed that a point at (-1.5, 1.5) would seem not to belong to the oval shaped scatter, even though the individual values of -1.5 and 1.5 on either variable are not unusual. Such a point would be in the extreme lower tail of a dotplot of the products of the standardized variables, confirming from this definition of correlation that the point is unusual. Note that the addition of this one point would reduce the sample correlation from .50 to .38.
18 The regression line for predicting the verbal score
from the math score is, in the standardized scale,
Figure 4. Regression Line and Point-Fit Line. The point-fit line is "closest" to the data points.
19 As a final step in using the
20 Most textbooks introduce correlation and regression via formulas. For example, Moore and McCabe (1993, p. 164) and Wild and Seber (2000, p. 540) use the n - 1 definition of the correlation and define the regression slope in terms of the unstandardized variables (Moore and McCabe 1993, p. 123; Wild and Seber 2000, p. 518).
21 The explicit interpretation of correlation in terms of distance does not appear in the "Thirteen Ways" summary article by Rodgers and Nicewander (1988), nor in the follow-up papers by Rovine and von Eye (1997) and Nelsen (1998), even though this interpretation appears to be one of the most intuitive.
22 When data are expressed in standardized form, correlation and regression methods can be described very simply. The difference between fitting a line to points and regression is clarified by this simpler presentation. The use of n - 1 in formulas for the standard deviation and the correlation coefficient is an unnecessary complication.
The author would like to thank the referees, the editor, and an associate editor for helpful comments on the first draft.
Cleveland, W. S. (1993), Visualizing Data, Summit, NJ: Hobart Press, p. 89.
Freedman, D., Pisani, R., and Purves, R. (1998), Statistics (3rd ed.), New York: Norton.
Minitab Inc. (1994), MINITAB Reference Manual, Release 10Xtra, State College, PA: Author.
Moore, D. S., and McCabe, G. P. (1993), Introduction to the Practice of Statistics (2nd ed.), New York: Freeman.
Nelsen, R. B. (1998), "Correlation, Regression Lines, and Moments of Inertia," The American Statistician, 52, 343-345.
Rodgers, J. L., and Nicewander, W. A. (1988), "Thirteen Ways to Look at the Correlation Coefficient," The American Statistician, 42, 59-66.
Rovine, M. J., and von Eye, A. (1997), "A 14th Way to Look at a Correlation Coefficient: Correlation as the Proportion of Matches," The American Statistician, 51, 42-46.
Weldon, K. L. (1986), Statistics: A Conceptual Approach, Englewood Cliffs, NJ: Prentice-Hall, p. 144.
Wild, C. J., and Seber, G. A. F. (2000), Chance Encounters: A First Course in Data Analysis and Inference, New York: Wiley.
K. L. Weldon
Department of Mathematics and Statistics
Simon Fraser University
8888 University Drive
Burnaby, BC, Canada V5A 1S6
JSE Homepage | Subscription Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications