 4
4Sharon Lawner Weinberg
New York University
Sarah Knapp Abramowitz
Drew University
Journal of Statistics Education v.8, n.2 (2000)
Copyright (c) 2000 by Sharon Lawner Weinberg and Sarah Knapp Abramowitz, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the authors and advance notification of the editor.
Key Words:
Statistical education; Teaching statistics; Using real datasets and real situations.Five case studies based on real situations and real data are presented for use in courses on research methodology and data analysis. Departing from the typical case study approach, students are asked to act as consultants to resolve the issues placed before them, prior to being given a solution. In generic terms, students are given a description of a real problem and a real dataset relevant to solving that problem and are asked for their advice on how the problem may be solved. This approach motivates students to take ownership of the problem at hand and provides them with the opportunities and experiences to use the tools of their education actively, rather than to merely acquire them.
1 The topic of teaching effectiveness at the university level has received much attention in recent years. At New York University (NYU), for example, the administration has charged its Educational Policies Committee with the task of defining teacher effectiveness and of creating opportunities at the university for its enhancement.
2 Of course, concerns about teaching effectiveness must, by definition, be linked to concerns about student learning. Quite simply, for teachers to be effective they must provide experiences and opportunities for students to reach the goals they have set for them.
3 Although particular goals will vary from course to course and from year to year, many researchers have argued that, as teachers, we must direct students to develop confidence in their skills to use knowledge in order to expand their thinking and learning and to solve problems independently (Baron and Sternberg 1987; Bransford, Sherwood, Vye, and Rieser 1986; Ennis 1987; Nickerson 1987; Resnick 1987; Salomon and Perkins 1989; Schwartz 1987; Simon 1980; Sternberg 1985). They have also argued that in accordance with these goals, students must view knowledge as a set of tools to be applied in meaningful ways, rather than as inert and arbitrary procedures or facts to be memorized (Bransford and McCarrell 1974; Dewey 1910). Based on a discussion by Whitehead (1929), the Cognition and Technology Group at Vanderbilt University (1990) defines inert knowledge as "knowledge that can usually be recalled when people are explicitly asked to do so but is not used spontaneously in problem solving even though it is relevant" (p. 2).
4 Many of us who are involved in teaching research methodology and data analysis agree on the importance of providing our students with opportunities and experiences that give them the confidence and skill to solve problems independently. As such, we believe that inert knowledge is not useful knowledge. Our challenge is to find ways of presenting information to our students so that it is accessible, relevant, applicable, and even vital to their own areas of interest.
5 One approach that has been used successfully by the Cognition and Technology Group at Vanderbilt (1990), and that we have been using independently in our own classes, is to create situations that permit students to understand the kinds of problems that experts in the field encounter as consultants and to also understand the knowledge that consultants use as tools for solving these problems. Because this approach anchors instruction in the context of authentic, problem-solving tasks, it is a form of what is called anchored instruction. Anchored instruction has been found to provide a more meaningful and stimulating learning experience than the more traditional, fact-oriented approach (Adams et al. 1988; Lockhart, Lamon, and Glick 1988).
6 The use of real data has been advocated for quite some time to enhance student learning in courses on data analysis and design (Goldman 1996; Singer and Willett 1990; Wilson 1992). As consultants and as consumers of the literature and media, we are exposed to a wealth of real problems and data to bring to the classroom to serve as case studies for students to analyze and solve. When asked to solve a real problem based on real data that is relevant to them, students become motivated to take ownership of the problem and to apply their problem-solving skills and knowledge base in an active way to reach a solution. By linking general principles to real problems that experts face as consultants and as consumers, we send a strong message to our students that such principles are relevant, applicable, and vital tools of our trade.
7 In this paper we present five case studies that are either based on real problems we have faced as consultants ourselves or on real data that is publicly available to exemplify general principles commonly taught in courses on research design and data analysis. We depart from the typical way in which case studies are presented in classrooms by the fact that we ask each student to act as a consultant to resolve the issues placed before him. Like the consultant, each student is expected to resolve the problem presented prior to being told how it was solved. Like the consulting situation, questions are posed in a more general and diffuse form. In generic terms, we describe the problem to students, give them a real dataset that we believe is relevant to solving the problem and ask them for their advice on how the problem may be solved. We ask each student to work independently to arrive at a solution. A more directed approach might ask students to carry out a specific statistical procedure on a given dataset. By contrast, our approach leaves the formation of the procedure for solving the problem up to the student himself, from beginning to end. In so doing, our approach motivates students to take ownership of the problem in the way a consultant takes ownership of a problem when asked to do so by a client. To capture the difference between the more typical case study approach and our approach, we follow the suggestion of one of our reviewers and call our case studies "active case studies."
8 The active case studies we describe are not specific to a single course or even a specific level. We have used them in our separate classes at both the graduate and undergraduate levels. A common feature of our classes, however, is their moderately small size of approximately 25 that allows for open class discussion. We believe that the positive effects we have observed using this approach will generalize to other situations and problems. There is no doubt that an interesting data or design problem is an important ingredient to that generalization. Another important ingredient, however, is the ability of the instructor to express to the class a genuine interest in obtaining the solution to the problem in much the same way a client expresses that interest to a consultant.
9 In the following sections of this paper, we give examples of five active case studies which we believe have helped to create an environment for our students where learning is memorable, knowledge is useful, and research design and data analysis are valued.
General Principle 1: "Pilot studies are almost always worth the time and effort. Carry out a pilot study if any facet of your design needs clarification." (Light, Singer, and Willett 1990, p. 213)
10 Students are presented with the following situation that illustrates General Principle 1. They are asked to consider the situation at home and to come to the next class with a well thought out solution. They are told that at the next class they will be called upon to present their solutions and to defend them.
I and two other NYU faculty members are the recipients of a large grant from NIDA, the National Institute of Drug Abuse, to study whether estimates of adolescent risk behavior calculated by such organizations as Monitoring The Future (MTF) are biased. MTF estimates of adolescent risk behavior are based, with some modification, on a one-stage sampling design. That is, MTF randomly selects a given number of cooperating high schools and distributes questionnaires to students in required classes in 10th grade. If MTF captures at least 70% of the students in a given school, it includes those questionnaires in its estimates of adolescent risk behavior and does not return on a later date to collect information from those who were absent or otherwise not present in the classroom on that day. If MTF captures less than 70%, it returns on another day to obtain additional responses. If, after the second attempt, the percentage captured is still less than 70%, MTF discards the data from that school on the rationale that fewer than 70% cannot represent well all those enrolled in 10th grade for that school.
Our grant is to study whether MTF estimates are biased by not including the information on the remaining 30% or more. Said differently, we question whether the 30% or more that are not present to take the questionnaire are systematically different in their risk behavior from those who are present. We have proposed a four-stage sampling design on twelve public high schools randomly selected from the total number of high schools in New York City. While the first two stages replicate the MTF procedure, the last two stages, stages 3 and 4, use an incentive to attract students to complete the questionnaire. Clearly, the use of an appropriate incentive is critical to our project to attract the chronically absent or cutting students. Without such incentive, the data for judging whether estimates of adolescent risk behavior based on modified single-stage sampling designs are biased will not be available to us.
We decide to subcontract out to you the task of determining the incentive that we should use at stages 3 and 4. Our budget allows us to spend no more than $15 per student. Because NIDA does not allow giving each student $15 in cash (they are concerned that some students will use the money to buy illegal substances), what is your proposal for determining an appropriate incentive?
11 At the next class meeting we began by asking for volunteers to begin the discussion of plausible solutions. Because all students had a chance to think through the issues of the problem at home, they came to class prepared to discuss and evaluate the potential strengths and weaknesses of each proposal suggested. The in-class discussion was lively and animated. Some students suggested gift certificates to Burger King or McDonald's. Others suggested tickets to baseball games and other sporting events. No one came up with the idea of tailoring the gift to a particular school or student body within a school, even though many of the objections raised by students concerned the proposed choice of a particular gift (the particular sporting event or restaurant chain). After all students who were interested in presenting their solutions had done so, we revealed what actually occurred in carrying out our research.
In order to determine what types of incentives would be most effective, even before the pilot study, we conducted a focus group with 12 students from a high school in the Lower East Side of Manhattan. The students all agreed that $15 gift certificates to Tower Records, a local music store, would serve as sufficient incentive for other students in the New York City area.
Our pilot study was conducted in two high schools, one in midtown Manhattan and the other in the Bronx. When incentives were distributed at these schools, we quickly learned that (1) Tower Records was not reachable via public transport in the Bronx, and (2) the students did not consider $15 enough to purchase something suitable. Due to the combination of these two factors, our response rates during the later parts of the study were not remotely close to what was originally expected. Accordingly, we decided to tailor the incentives to the school being surveyed.
Prior to the full-scale study, student representatives from each school were asked to complete an information sheet on directions to the school as well as what they considered to be an appropriate incentive. Responses included movie tickets to local theaters and gift certificates to Old Navy, a retail clothing store. Because movie tickets involved dealing with several different movie chains, we decided to use the gift certificate to Old Navy as our incentive. There is at least one Old Navy store in every borough of New York City (and all are near some form of public transportation).
Despite the "tailoring" of incentives, the issue of amount again became a problem. Students complained, quite frequently, that $15 was not enough to buy anything substantial. To determine whether the incentives were indeed the reason why response rates at stages 3 and 4 were so low, the amounts were doubled at three high schools. The results showed that doubling the amount to $30 increased response rates at stages 3 and 4, and especially at stage 4 (see Tables 1 through 4).
Table 1. Expected Rates of Response by Stage
|
Stage |
% of Students |
No. of Students |
No. of Students |
|
0 |
2,400 |
||
|
1 |
60.0% |
1,440 |
960 |
|
2 |
37.5% |
360 |
600 |
|
3 |
50.0% |
300 |
300 |
|
4 |
40.0% |
120 |
180 |
Table 2. Pilot Study Rates of Response by Stage Using $15 Tower Record Gift Certificates
|
Stage |
% of Students |
No. of Students |
No. of Students |
|
0 |
495 |
||
|
1 |
70.9% |
351 |
144 |
|
2 |
25.7% |
37 |
107 |
|
3 |
8.4% |
9 |
98 |
|
4 |
9.2% |
9 |
89 |
Table 3. Full-Scale Study Rates of Response by Stage Using $15 Old Navy Gift Certificates
|
Stage |
% of Students |
No. of Students |
No. of Students |
|
0 |
1,845 |
||
|
1 |
72.2% |
1,332 |
513 |
|
2 |
28.7% |
147 |
366 |
|
3 |
14.5% |
53 |
313 |
|
4 |
4.5% |
14 |
299 |
Table 4. Full-Scale Study Rates of Response by Stage Using $30 Old Navy Gift Certificates
|
Stage |
% of Students |
No. of Students |
No. of Students |
|
0 |
628 |
||
|
1 |
66.9% |
420 |
208 |
|
2 |
14.4% |
30 |
178 |
|
3 |
15.7% |
28 |
150 |
|
4 |
18.7% |
28 |
122 |
We learned from the pilot study that two main considerations in using incentives are amount and type. For our purposes, using $30 gift certificates in 15 schools (two in the pilot and 13 in the full-scale study) would have been too costly. However, tailoring the incentive to each school student body was possible and did have a positive effect.
12 Students were surprised to learn that we experienced a number of false starts in coming up with an appropriate incentive and saw how essential the pilot study was in this case. They expressed genuine appreciation for the now obvious importance of field testing critical aspects of a study before it is undertaken and became interested in the kind of pilot studies that they might conduct in relation to their own research studies, currently in the planning stages. Clearly, they were able to transfer their appreciation for the importance of a pilot study from this specific case to their own studies, suggesting that anchored instruction is not inconsistent with more generalized learning.
General Principle 2: "It should be remembered that numeric summaries are just that; they summarize characteristics of distributions. Thus, the analysis should begin with the data, not with summaries of the data." (Hartwig and Dearing 1979, p. 16)
13 Students are asked to consider for homework the following situation that illustrates General Principle 2 and to come to class prepared to present a plausible solution that they can defend.
In response to pressure from the federal government, the National Center for Education Statistics (NCES) designed the National Educational Longitudinal Study (NELS) to monitor the progress of student achievement in the U.S. In 1988 the NCES collected data on a sample of 25,000 cases selected randomly from the population of U.S. 8th graders. They also conducted two-year follow-ups in 10th grade, 12th grade, and two years post-secondary. One of the many variables recorded is grade point average through the highest grade attended. Based on the total number of cases from the Northeast and West who have values on this variable (2,027 from the Northeast and 3,014 from the West), we find that the median grade point average for students in the West is lower than that for students in the Northeast. In particular, the Northeast has a median grade point average of 3.51, while the West has a median grade point average of 2.76.
We are baffled by this result and hire you as our consultant to explain it to us. You may access the complete set of data at the computer lab.
14 At the next class meeting we asked for volunteers to explain our obtained results. We began with those students who did not refer to the actual dataset in coming up with their solutions. Once again, the discussion turned out to be quite lively. Many students presented explanations that revolved around issues of grade inflation, achievement motivation, academic preparedness, drop-out rates, ability, and even the sunny weather in the West! After these were presented, we then asked the few students who had examined the data to present their solutions. As they had learned, the true and most obvious explanation is revealed by the data themselves.
15 As startling as it may be, as shown in Table 5, at least two different grading scales or metrics were used by NCES to enter grade point average. One metric uses a scale from 0 to 4, where 4 represents a grade of A, 3 represents a grade of B, and so on. Another metric uses a percentage scale ranging from 0 to 100. The discrepancy in medians is an artifact of how these data were recorded and entered. Simply stated, schools from the Northeast use the 0 to 100 grading scale with greater relative frequency than schools from the West, which tend to use the 0 to 4 grading scale.
Table 5. Use of Different Grade Point Average Metrics by Region
Grade Point Average 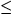 4 4 |
Grade Point Average > 4 | ||
| Northeast | 1,172 | 855 | 2,027 |
| West | 2,965 | 49 | 3,014 |
NOTE: It is not always possible to tell which grading scale was used! A grade point average of 4.5, for instance, could represent the 0 to 4 scale, with extra weighting for honors courses, or it could represent the percentage scale. Other values, such as 9.30, are not so easily explained. In addition, a small number of grade point averages in the dataset exceed 100.
Source: U.S. Department of Education, National Center of Education Statistics, National Educational Longitudinal Study (1988, 1990, 1992, 1994)
(Click here for the data and a description of the variables.)
16 The vast majority of students who did not review the data themselves to look for anomalies and irregularities and who relied instead on the medians alone to develop their elaborate explanations of cause clearly felt duped. They were genuinely surprised by the simplicity of the explanation of the finding, and, more importantly, they were surprised that a reputable organization such as the NCES would have measured a variable like grade point average on two very different scales. This example illustrated quite clearly to students that data analysts must not only be concerned about the usual types of data anomalies and irregularities, but also about even more basic and unusual types of anomalies as well. The degree of surprise expressed by students suggests how powerfully the point had been made; they should remember this general principle well and interpret summary statistics with caution until a full description of the underlying data is known.
General Principle 3:
In constructing a summated rating scale, "response
choices are chosen so that they can be ordered along a
measurement continuum. Frequency varies from
nonoccurrence (none or never) to constant occurrence
(always or continually)" (Spector 1992,
17 We assigned the following homework problem that asked students to consult on a current project with which the senior author was involved as a consultant. The project concerned the evaluation of the effectiveness of a speech and language treatment program for individuals with aphasia.
Aphasia is an acquired communication disorder that impairs the ability to express oneself using speech and/or to understand speech. Aphasia may also affect one's ability to use writing or reading as a means of communication. Degree of impairment may range from mild to severe. The impact of aphasia on the quality of life for both the impaired person and his or her family is dramatic and devastating. Individuals with aphasia find themselves alienated from their communities and forced to negotiate a new relationship with the speaking world. Few are able to participate fully as members of their communities, and the majority remain socially isolated.
A program has been developed for people suffering from aphasia at a Speech-Language Pathology Department at a local Medical Center. This program provides 60 patients and their caregivers with speech-language pathology services and social service follow-up for a one-year period. It is hypothesized that such treatment will lead to positive increases in quality of life. The first ten items from the quality of life instrument along with a scale for their scoring, as given to us by the assistant to the director of this program, appear in Tables 6 and 7, respectively.
Table 6. Items from Quality of Life Scale
|
Activity |
|
Preparing main meals |
|
Washing up |
|
Washing clothes |
|
Light housework |
|
Heavy housework |
|
Local shopping |
|
Social occasions |
|
Walking outside (at least 15 minutes) |
|
Actively pursuing a hobby |
|
Driving a car/bus travel |
Table 7. Scale for Scoring
|
Coding |
|
1 = never |
|
2 = less than once per week |
|
3 = 1-2 times per week |
|
4 = 1-2 times in 3 months |
|
5 = 3-12 times in 3 months |
|
6 = weekly |
Based on a review of Tables 6 and 7, what data analytic issues would you address with the medical personnel who have hired you to help them to evaluate the effectiveness of their program on quality of life? In particular, how might the frequencies that define the scoring scale be changed to a different set of response choices that can be ordered along a measurement continuum?
18 Students were quick to identify potential problems with the scoring scale. In particular, they noted the fact that response choices as defined were not ordered along a measurement continuum. They noted that while response choices 1, 2, and 3 are on a continuum, and response choices 4, 5, and 6 are as well, as a set, 4, 5, and 6 do not follow the continuum defined by 1, 2, and 3. In particular, if the score of 3 is assigned to the frequency 1-2 times per week, it does not follow that a score of 4 is assigned to the frequency 1-2 times in 3 months. Students were convinced, as they should have been, that additional information on the validity of this scale needed to be obtained before any data analysis was carried out.
19 At this point, students were given a copy of the paper describing the quality of life scale (Holbrook and Skilbeck 1983). This paper contained information on the psychometric properties of the instrument. It also presented a scale for scoring the items that was actually different from what the program assistant had given us. In particular, the first two items (preparing main meals and washing up) were scaled by the categories never, less than once per week, 1-2 times per week, and most days. These categories were assigned the values 1 through 4, respectively. The remaining eight items were scaled by the categories never, 1-2 times in 3 months, 3-12 times in 3 months, and at least weekly. These categories were also assigned the values 1 through 4, respectively. Hence, both sets of categories were ordinal, as they should have been.
20 Guided class discussion focused on how a single set of categories could be used for all ten activities to understand the rationale for the test developer's choice of using two different sets of categories. One student suggested that perhaps both sets of categories could be viewed more generally in terms of the degree of similarity to normative behavior relative to each activity, under the assumption that the individuals taking this test perform these activities at the normative rate or less. In particular, because washing up is normally conducted on most days, the highest score of 4 is assigned to individuals who wash up on most days. Likewise, because local shopping is normally conducted at least weekly, the highest score of 4 is assigned to individuals who do their local shopping at least weekly. This led to a discussion of the definition of normative behavior and to further criticisms of these scales.
21 This authentic consulting situation showed students the importance of examining the underlying scales of measurement that individuals plan to use for data collection before such data are analyzed. It was an example that demonstrated clearly that when conducting data analyses, all data-related issues must be explored, including the validity of the measurement scales on which the data are based. Through this example, students began to appreciate how knowledge may be used actively to uncover truths about the phenomena they are studying -- that is, by beginning an analysis by scrutinizing the scores themselves and the scales that generated them.
General Principle 4: "A detailed description of the data, including possible anomalies, and an ample characterization of results, are critical components of any data analytic plan." (Weinberg and Abramowitz, in press, p. 1)
During the Fall 1998 semester, Mark McGwire and Sammy Sosa were involved in a tight race to break Roger Maris' 1961 home run record of 61 home runs hit in a single season. Yet, during the final phase of the competition, Mark McGwire received the lion's share of media attention. For those of us who were captivated by this competition and who had not followed baseball seriously in previous seasons, the difference in media attention was perplexing.
While one could explain the attention given to Mark McGwire as due, in part, to the fact that McGwire led Sosa in home runs during the season (although not by very much at times), it is also possible that their past season home run histories could have contributed to the difference in attention they received.
Consider yourself hired as a consultant to come up with answers to this question. For your information, we have attached the home run and at-bats histories of both players in
Table 8 . During the 1993 and 1994 seasons, Mark McGwire was injured early in the season and was removed from the lineup, as reflected by his low number of at-bats. During the 1992 season, Sosa was injured early in the season and also was removed from the lineup, as reflected by his low number of at-bats. Sosa joined the major leagues in 1989, while McGwire joined in 1986.
Table 8. The McGwire and Sosa Home Run and At-Bats History from the Time They Were Rookies to the Present
|
Season |
Sosa Home Runs |
Sosa At-Bats |
McGwire Home Runs |
McGwire At-Bats |
|
1986 |
. |
. |
3 |
53 |
|
1987 |
. |
. |
49 |
557 |
|
1988 |
. |
. |
32 |
550 |
|
1989 |
4 |
183 |
33 |
490 |
|
1990 |
15 |
532 |
39 |
523 |
|
1991 |
10 |
316 |
22 |
483 |
|
1992 |
8 |
262 |
42 |
467 |
|
1993 |
33 |
598 |
9 |
84 |
|
1994 |
25 |
426 |
9 |
135 |
|
1995 |
36 |
564 |
39 |
317 |
|
1996 |
40 |
498 |
52 |
423 |
|
1997 |
36 |
642 |
58 |
540 |
|
1998 |
66 |
643 |
70 |
509 |
(Click here for a text file of the data.)
22 Students enjoyed this problem because of the currency of the issues it raised. The data related directly to what were then current headlines in the daily newspapers, and they provided meaning for understanding those headlines. Discussion about the data was animated, and even the students in the class who were less inclined, in general, to be captivated by sports data, were captivated in this case because of the history-making nature of the event. This assignment allowed students to begin to appreciate the value of statistics as a set of relevant and vital tools for answering interesting questions that relate to real situations making national headlines.
23 Students raised issues related to data entry (defining the variables to enter, including grouping variables, in the dataset) and data screening (whether to include the rookie seasons and the injury-shortened seasons). They raised issues related to the creation of new variables (the ratio of at-bats to home runs, indicating the number of times a player is at bat for each home run he hits) that are transformations of existing variables in the dataset. They were also able to observe that media coverage was better predicted by using measures of consistency and location together than by using either measure alone.
General Principle 5: Predictors should be included in a design because they are substantively interesting or important. They should also be incorporated "for two other reasons: (1) to disentangle the effects of the substantive predictors from the effects of other, less-important, 'background' characteristics; (2) to determine whether two (or more) predictors interact in their relationship with the outcome variable" (Light, Singer, and Willett 1990, p. 86).
24 Unlike the first four principles, General Principle 5 was the focus of an entire one-semester course on data analysis, rather than of a single example. This approach was similar to "the generation of cases and management games" (Welsch 1992, p. 303) used by business schools.
You are given 534 observations on 11 variables including hourly wage, occupational status, years of experience, years of education, sex, union membership, marital status, and region of residence, sampled from the Current Population Survey of 1985 (Berndt 1991). Access these data, submitted to StatLib by Therese A. Stukel, Dartmouth College, from the academic computing facility. Assume you are hired as a consultant to determine whether there exists a gender gap in wages. What data analytic issues are salient, and what data analytic strategies would you use?
(Click here for the data and a description of the variables.)
25 Beginning with a simple independent groups t-test, students spend the semester exploring issues relevant to the question of interest and analyzing these data by taking into account the issues raised. As noted by Welsch (1992), "as the complexity of the problem is revealed, increasingly sophisticated statistical procedures can be introduced and in the end most of what is required in either a basic or advanced course can be introduced" (p. 303). In this particular case, issues regarding confounding, transformations, multicollinearity, categorical variables, unbalanced ANOVA designs, interactions, simple effects, and model building strategies are discussed and illustrated in the course of the semester. Students liked the fact that a single relevant and interesting question was addressed and that a single set of real data was used throughout.
26 Given that the data were real, and the issue they raise was timely (a gender gap in wages), students were highly motivated to uncover the "true" answer to the question posed. Using one set of data throughout lent cohesiveness to the structure of the course and gave students a fuller understanding of the issues one faces as a data analyst. Having students role-play as consultants added to their motivation to analyze these data to uncover their hidden meaning. Students were evaluated through a series of interim and final reports written to the employer (i.e., instructor) on latest findings. Hence, skills in the communication of statistical results were enhanced as well. In addition to the obvious statistical knowledge learned through active exploration, the course served well to train students in what it is like to be a statistical consultant on an important and timely issue.
27 These examples illustrate how general principles typically read in texts or recited in class can come alive in the classroom through the use of real data or situations viewed by students as interesting and important. The senior author was personally involved in the first two situations as a consultant, and, as a result, students attributed a high level of importance to these situations. The remaining three situations addressed issues (an ongoing home run race, a comparison of grade point averages, and a gender gap in wages) that were considered, by their timeliness, worthy of being solved. Because students were asked to serve as "consultants" to these situations, they were further motivated to take ownership of these problems and to find appropriate solutions. By role-playing as consultants, students appeared to be more willing to volunteer their solutions to the instructor and the class. By role-playing as the client, the instructor was able to create a collegial and friendly atmosphere in the classroom where students freely discussed the issues and the approaches they used to address them. Although no explicit measures were used to evaluate the effectiveness of this approach, other less formal approaches based on instructor observations of student and classroom behavior proved helpful. The level of student participation in classroom discussions, the nature of student questions asked, and the connections made by students between the situations presented in class and their own emerging research studies all contributed to a strong positive impression that the approach was effective in its ability to anchor student learning, and to anchor it well.
28 We believe that as long as we, as instructors, are sensitive to the many opportunities we have to convert real world problems into active case studies for classroom use, the effort and preparation required to provide this type of experience should be reasonably low. We invite all interested readers to make use of the situations and data presented in this paper.
29 In sum, this approach seeks to develop a deep understanding of the principles of our field by combining directed instruction with opportunities for active and critical exploration of problems that exemplify such principles. Our ultimate goal is to support our students in their creation of a knowledge base that is relevant rather than extraneous, that is useful rather than inert. We must challenge ourselves as instructors of research methodology and data analysis to collect timely and real situations of substantive and methodological interest and to use these situations in class. In so doing, our students will learn from them and from us what it is to use the tools of their education actively, rather than to merely acquire them. Through this approach, our aim is to encourage our students to "build an increasingly rich implicit understanding of the world in which they use the tools and of the tools themselves" (Bradstreet 1996, p. 74).
Adams, L., Kasserman, J., Yearwood, A., Perfetto, G., Bransford, J., and Franks, J. (1988), "The Effects of Fact Versus Problem-Oriented Acquisition," Memory & Cognition, 16, 167-175.
Baron, J. B., and Sternberg, R. J. (1987), Teaching Thinking Skills, New York: Freeman.
Berndt, E. R. (1991), The Practice of Econometrics, New York: Addison-Wesley.
Bradstreet, T. E. (1996), "Teaching Introductory Statistics Courses So That Nonstatisticians Experience Statistical Reasoning," The American Statistician, 50, 69-78.
Bransford, J. D., and McCarrell, N. S. (1974), "A Sketch of Cognitive Approach to Comprehension," in Cognition and the Symbolic Processes, eds. W. Weimer and D. Palermo, Hillsdale, NJ: Erlbaum, 299-303.
Bransford, J. D., Sherwood, R., Vye, N. J., and Rieser, J. (1986), "Teaching Thinking and Problem Solving: Research Foundations," American Psychologist, 41(10), 1078-1089.
Cognition and Technology Group at Vanderbilt (1990), "Anchored Instruction and Its Relationship to Situated Cognition," Educational Researcher, 19, 2-10.
Dewey, J. (1910), How We Think, Lexington, MA: Heath.
Ennis, R. (1987), "A Taxonomy of
Critical Thinking Dispositions and Abilities," in
Teacher Thinking Skills: Theory and Practice,
eds. J. Baron and R. Sternberg, New York: Freeman,
Goldman, R. N. (1996), "Trends in
Introductory Applied Statistics Courses: Techniques," in
Proceedings of the Section on Statistical Education,
American Statistical Association,
Hartwig, F., and Dearing, B. E. (1979), Exploratory Data Analysis, Newbury Park, CA: Sage Publications.
Holbrook, M., and Skilbeck, C. E. (1983), "An Activities Index for Use With Stroke Patients," Age and Ageing, 12, 166-170.
Light, R. J., Singer, J. D., and Willett, J. B. (1990), By Design: Planning Research on Higher Education, Cambridge, MA: Harvard University Press.
Lockhart, R. S., Lamon, M., and Glick, M. L. (1988), "Conceptual Transfer in Simple Insight Problems," Memory & Cognition, 16, 36-44.
Nickerson, R. S. (1987), "Why Teach Thinking?," in Teacher Thinking Skills: Theory and Practice, eds. J. Baron and R. Sternberg, New York: Freeman, pp. 27-37.
Resnick, L. (1987), Education and Learning to Think, Washington, DC: National Academy Press.
Salomon, G., and Perkins, D. N. (1989), "Rocky Road to Transfer: Rethinking Mechanisms of a Neglected Phenomenon," Educational Psychologist, 24(2), 113-142.
Schwartz, R. J. (1987), "Teaching for Thinking: A Developmental Model for the Infusion of Thinking Skills Into Mainstream Instruction," in Teacher Thinking Skills: Theory and Practice, eds. J. Baron and R. Sternberg, New York: Freeman, pp. 106-126.
Simon, H. A. (1980), "Problem Solving and Education," in Problem Solving and Education: Issues in Teaching and Research, eds. D. T. Tuma and R. Reif, Hillsdale, NJ: Erlbaum, pp. 81-96.
Singer, J. D., and Willett, J. B. (1990), "Improving the Teaching of Applied Statistics: Putting the Data Back Into Data Analysis," The American Statistician, 44, 223-230.
Spector, P. E. (1992), Summated Rating Scale Construction: An Introduction, Newbury Park, CA: Sage Publications.
Sternberg (1985), Human Abilities: An Information-Processing Approach, NY: Freeman.
Weinberg, S. L., and Abramowitz, S. K. (in press), Statistics for the Behavioral Sciences (2nd ed.), London: Cambridge University Press.
Welsch, R. E. (1992), "Invited Comment: A Response to Statistical Consulting Is Scholarship," The American Statistician, 46, 302-304.
Whitehead, A. N. (1929), The Aims of Education, New York: MacMillan.
Wilson, W. J. (1992), "Statistical Consulting Is Scholarship," The American Statistician, 46, 295-298.
Sharon Lawner Weinberg
70 Washington Square South
Room 1202
New York University
New York, NY 10012
Sarah Knapp Abramowitz
Department of Mathematics and Computer Science
Drew University
Madison, NJ 07940
JSE Homepage | Subscription Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications