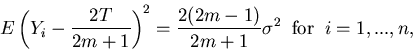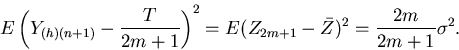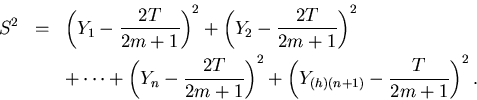Journal of Statistics Education, V8N2: Paranjpe
How Many Words in a Dictionary? Innovative Laboratory
Teaching of Sampling Techniques
S. A. Paranjpe and Anita Shah
The University of Pune, India
Journal of Statistics Education v.8, n.2 (2000)
Copyright (c) 2000 by S. A. Paranjpe and Anita Shah, all
rights reserved. This text may be freely shared among
individuals, but it may not be republished in any medium
without express written consent from the authors and
advance notification of the editor.
Key Words: Active learning; Practicals;
Sample surveys; Statistics.
Abstract
In Indian Universities, courses titled 'Statistics
Practical' usually involve only numerical evaluation.
There is very little scope for independent thinking and
decision making on the part of the students. We report here
our experience of teaching a practical course on sampling
techniques in a different way. On the whole, it was an
encouraging exercise.
1. Introduction
1 Reorganizing the contents of a statistics course or
changing the methods of teaching a course is a continuous
process. Fesco et al. (1996) discuss
why the typical course on survey sampling should be
restructured and how it can be done to suit the needs of
the society. Their discussion concerns a heterogeneous
group of students. In a university setting, students in a
master's degree course may be a homogeneous group. This
article discusses how the current syllabus can be taught
using a different approach to provide students with
practical experience, helping the material to come
alive.
2 In Indian Universities, statistics programs include
distribution theory, statistical inference, design of
experiments, and sampling theory of surveys as the core
courses. The classroom teaching of these courses mostly
involves derivation of formulae and proofs of theorems,
while numerical examples, if any, are on a Lilliputian
scale. The scale is small because large datasets cannot
be handled in classrooms, and, until recently, computer
facilities were very limited.
3 So-called 'practical' courses in statistics are
expected to play a role complementary to the theory
classes. The goals of an ideal practical course can be
set out as follows:
- Verifying empirically theoretical results like
the central limit theorem and the weak law of large
numbers. One can compare this to laboratory verification
of known 'laws' in a physics practical.
- Developing computational skills such as fitting
a specified model to a given dataset.
- Undertaking exploratory analysis in a given
situation where the answer is known to the teacher, but
unknown to the students.
- Handling a situation completely unknown to both the
teacher and the student and preparing a small project
report based on exploration and analysis.
4 At present, probably not many of us go beyond the first
two goals listed above. Unfortunately, there is very
little scope in the assignments related to goals (1) and
(2) for students to think independently. As a result, our
practicals become boring and uninteresting. Students just
end up plugging numbers into given formulae and writing
reject/accept H0 as their 'conclusion'
without bothering to think about what H0
is! Hence, alternative ways of conducting the practical
courses must be developed. We report here our experience
with one such attempt.
5 Any move towards changing this situation requires
strong motivation on the part of teachers, reasonable
flexibility in the student evaluation system, support from
colleagues, and, most importantly, students' cooperation
and enthusiasm. We present here our ideas, difficulties
encountered by the students, and their responses to a
'practical' on sample surveys. Our M.Sc. program consists
of 20 one-semester courses. This study forms one-half of a
semester course.
6 Considering the relative weight of this course in the
whole program and the time available for this study, a real
life problem involving field work was not feasible. Hence a
pseudo real life situation was considered.
2. The Case Study
2.1 Objective
7 In a routine practical course on sample surveys, we
assign a different set of questions for each session
devoted to a topic, e.g., cluster sampling or simple random
sampling without replacement (SRSWOR). Each session is two
and a half hours long. The total time spent on the exercise
described below was 8 to 10 sessions of two and half hours
each over a period of five weeks. In our changed format,
we set a common goal for the entire topic of sample
surveys. The goal was estimating the total number of words
in the Concise Oxford Dictionary (9th edition).
8 The broad objective to be achieved was as follows:
Empirical comparisons of different sampling strategies are
to be made, and the sampling variance associated with each
strategy is to be studied. Standard textbooks on sampling
theory like Murthy (1967), Cochran (1977), and Sukhatme, Sukhatme, Sukhatme, and Asok
1984) discuss situations under which one strategy
should do better than another. The exercise gives the
students a chance to empirically verify these comments.
The question set for this exercise is given as Appendix A.
2.2 Work Load for Students
9 Each student counted the number of words on 50 pages
for each of seven sampling strategies. In addition, for the
ratio and regression methods of estimation, the student had
to record an auxiliary variable. Hence, a student counted
words on 450 pages, a substantial amount of manual work.
Thus the students generated data instead of passively
receiving it. This gave them an opportunity to appreciate
difficulties in data generation.
10 For each sample drawn, the student calculated the mean
number of words per page and then estimated the population
total and its standard error. The formulae were not
provided ready-made. Instead, all prescribed textbooks
were made available, and students were asked to find and
use the appropriate formulae. This forced them to browse
through the books and hence increased the group
discussions about notational differences. Further, each
student had to draw a different sample. This helped in
overcoming one more difficulty. In our usual practical
setup where each student has the same question and the same
dataset, students are tempted to copy the answers. This was
not possible in the modified setup.
2.3 Protocol
11 The 'sampling unit' was defined to be one page of the
dictionary. Thus pages 1 to 1632 made up the 'sampling
frame.' The characteristic under study was a 'word.'
12 The first difficulty we encountered was the definition
of 'word.' Various possibilities include the
following:
- Head-word or main-word: Every word that starts at
the extreme left of the column on a page. Thus on page
number 509, one head-word is 'fist.'
- Words in bold type: These include head-words and
words derived from them like nouns, adjectives, and
adverbs. For example, words derived from 'fist' are
'fisted,' 'fistful,' and 'make a good fist.'
- Words and meanings: The back cover of the
dictionary claims that it contains 140 thousand 'meanings'
and two million 'texts of words.' As an illustration, we
can see that there are three meanings for the word 'fist.'
So along with meanings of the derived words, the count by
this definition is seven.
13 It was not obvious which definition one should use.
Hence a pilot survey of ten pages was done using the first
definition, which led to an estimate of 70 thousand words
in the dictionary, approximately half the value claimed.
When all bold-type words were counted, the estimate rose
to 110 thousand. Hence, the second definition was thought
to be more appropriate and was adopted for further work.
The pilot study also suggested that there could be some
relationship between number of head-words and number of
bold-type words on a page. This information was useful in
illustrating ratio and regression methods of estimation.
2.4 Generation of Random Samples
14 The following seven sampling strategies were used in the exercise.
- SRSWOR: Let R be a random uniform number from
U(0,1). Then IR = Int(1632 ×
R) + 1 is a random integer between 1 and 1632
indicating the page number to be sampled.
- Stratified Sampling: Natural stratification of the
dictionary is by letters of the alphabet, resulting in 26
strata. But some of these strata, namely J, Q, X, Y, and Z,
are so small that a sample of size 50 with proportional
allocation may never include a page from these strata. Table 1 shows the sample size that would
be chosen from each of these strata using a total sample
size of 50.
Table 1. Stratum Size and Sample Size for the Five Smallest Strata for Stratified Sampling with a Total Sample Size of 50
| Stratum |
Stratum size (Ni) |
Sample size (ni) |
| J |
13 |
0.4 |
| Q |
10 |
0.3 |
| X |
2 |
0.1 |
| Y |
6 |
0.2 |
| Z |
4 |
0.1 |
Hence, these letters were combined to form one stratum
of size 35 with ni = 1, giving a
total of 22 strata. Table 2 lists the
strata, their sizes, and the corresponding sample sizes.
The column of sample sizes contains some entries that are
fractional numbers. We can solve this problem by treating
each of the two columns on a page as an individual unit. We
note that in most cases the observation (i.e., count of
words) is recorded only for the whole page. The count is
recorded for half pages only when the sample size is
fractional. If ni = 1, we cannot
estimate the within stratum variation.
The rounding of the sample size was done using the
following ad hoc rule.
Let
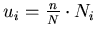 be the fractional sample size calculated. Then, if the
fractional part of ui is between 0
and 0.25, it is rounded to 0; between 0.25 and 0.75, to .5;
and between 0.75 and 1.00, to 1. Using this rule, the
estimate of the population total and its standard error
required a modification that is discussed in Appendix B.
be the fractional sample size calculated. Then, if the
fractional part of ui is between 0
and 0.25, it is rounded to 0; between 0.25 and 0.75, to .5;
and between 0.75 and 1.00, to 1. Using this rule, the
estimate of the population total and its standard error
required a modification that is discussed in Appendix B.
Table 2. Stratum Sizes and Sample Sizes for
Stratified Sampling with a Total Sample Size of 50
| Stratum |
Stratum size (Ni) |
Sample size (ni) |
| A |
89 |
2.5 |
| B |
91 |
3 |
| C |
156 |
5 |
| D |
88 |
2.5 |
| E |
56 |
1.5 |
| F |
72 |
2 |
| G |
56 |
2 |
| H |
62 |
2 |
| I |
54 |
1.5 |
| K |
18 |
0.5 |
| L |
59 |
2 |
| M |
86 |
2.5 |
| N |
35 |
1 |
| O |
43 |
1.5 |
| P |
138 |
4 |
| R |
83 |
2.5 |
| S |
205 |
6.5 |
| T |
96 |
3 |
| U |
35 |
1 |
| V |
26 |
1 |
| W |
48 |
1.5 |
| J, Q, X, Y, Z |
35 |
1 |
- Cluster Sampling: If the letters of the alphabet are
considered as clusters, then some clusters are too large
(like C) or too small (like Q). Hence, it was decided to
arbitrarily define every set of five consecutive pages to
be a cluster. Thus there would be 326 full clusters and
one cluster with two pages. Of these, ten clusters were
selected using SRSWOR, and words in the chosen sets of five
pages were counted.
- Systematic Sampling: If N denotes the total
number of pages and n the sample size, then let
K =
![$\left[ \frac{N}{n}\right] = 32$](par.img3.gif) .
A random digit R is generated between 1 to 32, and
the pages numbered R + 32m,
m = 0, ..., 49 form the sample. For example, if
R is 9, then pages 9, 41, 73, 105, ..., and 1577
form the sample.
.
A random digit R is generated between 1 to 32, and
the pages numbered R + 32m,
m = 0, ..., 49 form the sample. For example, if
R is 9, then pages 9, 41, 73, 105, ..., and 1577
form the sample.
- Two-Stage Sampling: Strata as defined for stratified
sampling were considered as first stage units, and five
strata were selected using the Midzuno scheme (see Sukhatme et al. 1984). From each of
the selected first stage units, ten pages were selected by
SRSWOR as second stage units.
- and 7. Ratio and Regression Methods: A sample
of size fifty was drawn by SRSWOR and head-words (X)
and bold-type words (Y) were counted from each
page.
2.5 Estimation of Standard Errors
15 For the SRSWOR and systematic sampling strategies and
the ratio and regression methods of estimation, standard
formulae were available in the textbooks. Since fractional
sample sizes were used in stratified sampling, the
estimator of the population total and its standard error
had to be modified suitably. Such small modifications are
inevitable when one drifts away from standard problems.
Because the derivation of that formula is not the main goal
of this article, we give the details in Appendix B.
16 For cluster sampling, multiple clusters were observed,
and an ANOVA table could be prepared to obtain estimates of
within and between cluster variation. These were then used
to estimate the standard error.
17 For two-stage sampling, the formula for the variance
of the estimator was not available because the first stage
units were drawn by the Midzuno scheme and the second stage
units by SRSWOR. Students therefore recognized the merit of
adopting an alternative two-stage sampling scheme.
3. Results and Discussion
18 The discussion of results below emphasizes the
learning process, rather than just reporting the outcome of
the sample survey. All students showed interest in the
whole exercise. They came up with interesting questions --
statistical and otherwise -- which does not usually happen
in our courses. No textbook solutions were available. An
example of a question asked was: "On the first page of the
dictionary 'A' appears as a bold-type word 16 times. Why
should these be treated as 16 separate words?"
19 Such difficulties were solved by group discussions.
Hence it became an interactive process. As teachers, we
were looking at the study as a whole. This led to some
interesting observations that were also discussed in the
group.
20 As this was our first experience with the exercise,
our involvement was very high. From results submitted by
the students, we did a sample check of two pages per
strategy per student. Thus we ended up counting words on
280 pages. In the case of the ratio and regression methods,
the population total of X (head-words) was needed,
which we estimated by counting head-words on about 500
pages. Thus the physical work for the teachers was
considerable. But this involvement enabled informed
interaction with students regarding the data collection.
Based on all the results, students gave a group seminar at
the end of the course in which findings based on
calculations done by the teachers were also discussed.
21 Table 3 shows a typical summary
prepared by a student. In this particular case, cluster
sampling had the smallest standard error, and systematic
the largest. The others -- namely, SRSWOR, stratified,
ratio, and regression -- appear fairly equivalent in terms
of empirical precision.
Table 3. Number of Words (× 10-5) Estimated by Different Sampling Schemes and Estimated
Standard Errors (× 10-5)
| Sampling scheme |
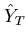 |
s.e. 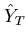 |
95% CI |
| SRSWOR |
1.09 |
0.026 |
(1.01, 1.11) |
| Stratified |
1.08 |
0.024 |
(1.04, 1.14) |
| Cluster |
1.11 |
0.007 |
(1.09, 1.12) |
| Systematic |
1.15 |
0.192 |
(0.78, 1.53) |
| Two-Stage |
1.09 |
* |
* |
| Ratio |
1.08 |
0.028 |
(1.02, 1.13) |
| Regression |
1.07 |
0.022 |
(1.03, 1.11) |
* Standard error and hence CI could not be obtained.
22 Table 4 gives the estimates for
the various sampling schemes for all students. From Table 4
the following points can be noted.
- One student (9508) reported extreme estimates. For
four strategies, he produced the lowest values, and for
systematic sampling, the highest. This unusual circumstance
could have been due to an incorrect method of counting
words. This occurrence was used as an excuse to discuss the
role of non-sampling errors in sample surveys.
- Empirical results indicate that variation across
samples is greater for systematic and two-stage sampling
than for the other schemes.
- All the estimates were around 100 to 120 thousand.
This raises a concern about why all 20 students
underestimated the number of words. The question arises
whether the bias could be due to the definition of
'word.'
Table 4. Estimates of Total Number of Words
(× 10-5) in the Concise Oxford
Dictionary
| Student Number |
SRSWOR |
Stratified |
Cluster |
Systematic |
Two-Stage |
Ratio |
Regression |
| 9403 |
1.08 |
1.07 |
1.05 |
1.14 |
1.08 |
0.99 |
1.01 |
| 9429 |
1.07 |
0.95 |
1.07 |
1.03 |
0.97 |
0.99 |
1.02 |
| 9431 |
1.03 |
1.00 |
1.12 |
1.14 |
1.06 |
1.03 |
1.08 |
| 9432 |
0.99 |
1.07 |
1.10 |
1.09 |
1.10 |
1.09 |
1.09 |
| 9443 |
1.11 |
1.07 |
1.06 |
1.38 |
1.11 |
1.08 |
1.09 |
| 9502 |
1.04 |
1.10 |
0.98 |
1.33 |
1.13 |
1.07 |
1.08 |
| 9503 |
1.09 |
1.11 |
1.08 |
1.09 |
1.14 |
1.07 |
1.08 |
| 9508 |
0.86 |
0.99 |
0.97 |
1.41 |
1.05 |
0.98 |
0.98 |
| 9509 |
1.10 |
1.09 |
1.10 |
1.12 |
1.03 |
1.06 |
1.08 |
| 9510 |
1.17 |
1.09 |
1.10 |
1.11 |
1.16 |
1.07 |
1.08 |
| 9513 |
0.87 |
1.04 |
1.10 |
1.10 |
1.15 |
1.06 |
1.06 |
| 9514 |
1.10 |
1.00 |
1.12 |
1.09 |
1.18 |
1.03 |
1.03 |
| 9517 |
1.10 |
1.12 |
1.09 |
1.11 |
1.13 |
1.04 |
1.06 |
| 9518 |
1.12 |
0.98 |
1.01 |
1.07 |
1.11 |
1.07 |
1.10 |
| 9529 |
1.02 |
0.98 |
1.02 |
1.07 |
1.04 |
0.99 |
1.01 |
| 9532 |
1.11 |
1.06 |
1.12 |
1.06 |
1.19 |
1.08 |
1.09 |
| 9534 |
1.10 |
1.06 |
1.03 |
1.12 |
1.11 |
1.10 |
1.12 |
| 9536 |
1.07 |
1.05 |
1.13 |
1.07 |
1.02 |
1.07 |
1.12 |
| 9540 |
1.17 |
1.16 |
1.13 |
1.13 |
1.24 |
1.11 |
1.15 |
| 9545 |
1.09 |
1.08 |
1.11 |
1.15 |
1.09 |
1.08 |
1.07 |
| Average |
1.06 |
1.05 |
1.07 |
1.14 |
1.10 |
1.05 |
1.07 |
Empirical
standard error |
0.08 |
0.05 |
0.05 |
0.10 |
0.06 |
0.04 |
0.04 |
Corrected
average |
1.41 |
1.40 |
1.42 |
1.51 |
1.47 |
1.40 |
1.41 |
23 To check if the definition of 'word' was the cause of
the underestimation, the following exercise was done. This
also gave an opportunity to discuss ratio and regression
methods. A random sample of 160 pages was drawn by SRSWOR
(roughly a 10% sample). Each student counted the number of
bold-type words (yi) and number of
'meanings' (wi) on 8 pages. After
pooling the data for 160 pages, a correction factor was
estimated:
All estimates were corrected using this factor to get an
estimate of the number of 'meanings.'
24 Averages of these corrected estimates for 20 samples
are given in the last row of Table 4.
We see that these values (except for systematic and
two-stage sampling) are very close to the claim in the
dictionary, which means that the third definition of 'word'
would have been more appropriate. This helped students
realize, somewhat dramatically, how a definitional issue
may be far more important than any amount of fine tuning of
statistical procedures. Details of how the correction
factor may affect the standard error were ignored.
25 In a typical course on sampling theory, we discuss the
number of distinct sampling units in a sample drawn with
replacement. In the present scheme, individual students
sampled without replacement. However, it is possible that
the same page could be selected by several students. Hence
we thought it would be interesting to ask, "How many
distinct pages did the students sample?" We checked this
only for the SRSWOR scheme.
26 All students together sampled 20 × 50 = 1000
pages. Of these, 717 were found to be distinct. With
n = 50 and N = 1632, the expected number of
distinct pages can be obtained as follows:
Probability that a given page will not be selected in a
sample of size n is
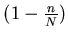 .
.
Probability that a given page will not be selected in
any of the 20 samples is
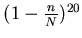 .
.
Expected number of pages not included in any of 20
samples is
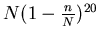 .
.
Expected number of pages included in at least one sample is
![$\hfill N[ 1 - (1 - \frac{n}{N})^{20}] \simeq 756 $](par.img9.gif) . .
|
(1) |
Variance of number of pages included in at least one sample is
![$\hfill N(1-\frac{n}{N})^{20} [ 1 - N (1 - \frac{n}{N})^{20}
+(N-1)(1-\frac{n}{N-1})^{20}] \simeq 108.71 $](par.img10.gif) . .
|
(2) |
27 Hence we can test the hypothesis of random selection
of pages, using the z test. We obtain 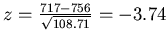 . This shows that the observed value is too
low. On careful scrutiny, it was suspected that one student
might have borrowed observations from other students and
put them together. On his own, he counted very few
pages.
. This shows that the observed value is too
low. On careful scrutiny, it was suspected that one student
might have borrowed observations from other students and
put them together. On his own, he counted very few
pages.
28 After deleting data from his sample, the observed
number of distinct pages for 19 samples turned out to be
705. The expected value 728 and variance 102.94 can be
calculated by replacing 20 by 19 in (1) and (2),
giving z = -2.27, which is again low. So we still
suspect that some students did not choose samples randomly,
but rather borrowed some observations from others.
29 Using the distinct pages, the following summary was prepared.
- The minimum number of words on a page was one for page number 89, the last page of the letter A.
- The maximum number of words on a page was 128 for page number 1535 of the letter U.
- Our observation is that, in general, all the pages
of the letter U have more words than the pages of other
letters. This gives an inflated estimate whenever there is
a page from the letter U in a sample. This suggests that
pages corresponding to the letter U may have an above
average number of words. A possible remedy is to take a
sample from the stratum corresponding to the letter U less
often than indicated by proportional sampling.
Alternatively, we can do a complete enumeration of words
starting with the letter U and then sample only from the
remaining 25 letters. This illustration was used to
discuss the importance of experience and close familiarity
with the population being sampled. It became obvious to
the class that the use of such knowledge can improve
estimates substantially.
- The mean number of words per page was
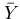 = 65.222 with standard deviation 13.795. The lower and
upper quartiles were Q1 = 58 and
Q3 = 72.
= 65.222 with standard deviation 13.795. The lower and
upper quartiles were Q1 = 58 and
Q3 = 72.
- The frequency distribution of the number of words
per page appears symmetric.
- A standard assumption in sample survey theory is
that Yi, the characteristic of
interest, follows a normal distribution. To verify this
assumption, a
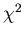 goodness of fit test was applied. This
showed that fit to the normal was not good. The maximum contribution to
goodness of fit test was applied. This
showed that fit to the normal was not good. The maximum contribution to 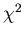 was from the modal class. The observed frequency (292) was
much larger than the expected frequency (196), indicating
more peakedness of the distribution. The lesson learned
was the need to be alert about the validity of assumptions.
The issue of how to deal with non-normality was not pursued.
It is also possible to study the sampling distributions of
the statistics computed by the students in a similar
manner. However, this was not done in the present
exercise.
was from the modal class. The observed frequency (292) was
much larger than the expected frequency (196), indicating
more peakedness of the distribution. The lesson learned
was the need to be alert about the validity of assumptions.
The issue of how to deal with non-normality was not pursued.
It is also possible to study the sampling distributions of
the statistics computed by the students in a similar
manner. However, this was not done in the present
exercise.
4. Conclusions
- Without the teacher's enthusiasm, such an exercise is
difficult.
- Once the teacher takes the initiative, most students
do respond positively.
- The boredom of routine computations can be reduced
by increasing students' participation in data generation,
which was a major component of this practical. However, if
the physical work involved is too heavy, the assignment can
be shared by a pair or group of students, as was done for
the correction factor calculations.
- The implementation of such an exercise is most
effective if the class size is small, say, ten.
- We feel that classroom teaching should be supported
by activities of this type wherever possible. The benefit
of such activities is illustrated by this student comment: "This is the first time that I have understood
what a stratum is and how it arises in a practical
situation."
- This approach can be problematic if we are exploring
a totally unfamiliar situation. We may have to face many
difficulties for which textbook solutions may not be
available. We must be open to discussions and subsequent
changes.
- Such activities give the students a chance to
handle at least a pseudo real life situation.
- Other real life problems that can be taken up in a similar way include
- Estimating the number of telephone subscribers in a
city using a directory.
- Estimating the total capital investment for
industries included in a stock exchange directory.
- Estimating the sex ratio using an electoral roll.
- The conduct of examinations was no more difficult
than routine examinations. A data file containing page
numbers and corresponding numbers of words was prepared
using information on distinct pages. This was treated as
the population. Each student was asked to draw two samples
-- one by SRSWOR and the other by one of the remaining
strategies. Students were asked to estimate the population
total and its standard error and to compare the two
strategies. The fact that we knew the true value helped in
assessment.
Acknowledgments
We wish to express our sincere thanks to Drs. A. P.
Gore, A. V. Kharshikar, and M. B. Rajarshi for help and
encouragement throughout the work. We also thank the
referees for their valuable comments which helped in
improving this material.
Appendix A: Assignment for the Exercise
Aim: To estimate the number of words in the
dictionary. We will study the following aspects of
sampling theory:
- For a given sampling strategy, how to estimate the
standard error of the estimate.
- How to compare the estimates given by different
strategies.
- To what extent principles, assumptions, and
theoretical results are applicable in a given practical
situation.
Observations and calculations: Use each sampling
strategy below to draw 50 random integers between 1 and
1632; these are the page numbers to be sampled. Count the
number of words in bold type on each page.
- List the random digit (i) and the number of words (yi).
- Estimate the total number of words.
- Estimate the standard error of your estimate.
- Obtain 95% confidence intervals for your estimates.
- Collect estimates from all others.
- Estimate the standard error of your estimates empirically.
Carry out (a) to (f) for each of the following sampling
strategies:
- Simple Random Sampling Without Replacement
Use
(i) the standard method of estimation, (ii) the ratio
method, and (iii) the regression method. For (ii) and
(iii), the auxiliary information X is the number of
head-words on a page.
- Stratified Random Sampling (standard method of
estimation)
- Cluster Sampling (standard method of estimation)
Treat five consecutive pages as a cluster and draw a sample
of ten clusters.
- Two-Stage Sampling (standard method of estimation)
Draw a sample of five strata out of 22, with probability
proportional to stratum size. From each letter chosen, draw
a sample of size ten using SRSWOR.
- Systematic Sampling (standard method of estimation)
Suppose N is the total number of pages in the dictionary. Let
![$k = \left[ \frac{N}{50} \right]$](par.img14.gif) .
Select a random number between 1 and k and draw a
systematic sample of size 50.
.
Select a random number between 1 and k and draw a
systematic sample of size 50.
Appendix B: Stratified Sampling -- Modification for
Fractional Sample Size
The formulae derived below apply to a single sample of
fractional sample size chosen from the N =
1632 pages in the dictionary. In stratified
sampling, these formulae are applied to each stratum, and
N refers to the size of the stratum. An estimated
total and its variance are computed for each stratum. To
estimate the population total, one must take the weighted
sum of stratum means with the stratum sizes as the
weights. The estimate of the standard error will have two
components, one for strata with integer sample sizes
(derived using textbook formulae) and one for strata with
fractional sample sizes (derived using the modified
formulae given below).
Let Y1, ...,
Yn,
Y(h)n+1 be a sample with
fractional sample size, i.e., Y1, ...,
Yn are observations on n
full units, and Y(h)n+1
denotes an observation on a half unit, i.e., one of the two
columns on the (n+1)th page. Let
Z1 and Z2 represent
observations on the two columns of the first unit,
Z3 and Z4
observations on the two columns of the second unit, etc.
Then, Z2m-1 and
Z2m are observations on the two
columns of the nth unit, and
Z2m+1 =
Y(h)n+1. We do not observe
Z1 and Z2 separately,
but rather Y1 = Z1 +
Z2, Y2 =
Z3 + Z4, etc.
Assume Z1, Z2, ...,
Z2m+1 are a random sample from a
normal distribution with mean
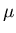 and variance
and variance 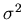 .
Then the population total is given by
.
Then the population total is given by 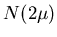 ,
where N = 1632. Consider
,
where N = 1632. Consider
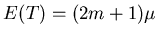 ,
and hence
,
and hence
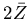 =
=
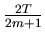 is an unbiased estimator of
is an unbiased estimator of 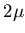 .
.
To obtain an estimator of var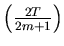 ,
consider
,
consider
Then,
and
Define
Then
It follows that S2/m2 is an unbiased estimator of var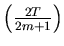 = var(
= var(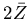 ) =
) = 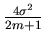 .
.
References
Cochran, W. G. (1977),
Sampling Techniques (3rd ed.), New York: John
Wiley and Sons.
Fesco, R. S., Kalsbeek, W. D., Lohr, S.
L., Scheaffer, R. L., Scheuren, F. J., and Stasny, E. A.
(1996), "Teaching Survey Sampling," The American
Statistician, 50, 328-340.
Murthy, M. N. (1967), Sampling Theory and Methods, Calcutta:
Statistical Publishing Society.
Sukhatme, P. V., Sukhatme, B. V.,
Sukhatme, S., and Asok C. (1984), Sampling Theory
of Surveys with Applications, Iowa State University
Press and Indian Society of Agricultural Statistics.
S. A. Paranjpe
saparanj@stats.unipune.ernet.in
Anita Shah
shah_anita@yahoo.com
Department of Statistics
The University of Pune
Pune - 411007
Maharashtra, India
JSE Homepage | Subscription
Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search
JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications
![]() be the fractional sample size calculated. Then, if the
fractional part of ui is between 0
and 0.25, it is rounded to 0; between 0.25 and 0.75, to .5;
and between 0.75 and 1.00, to 1. Using this rule, the
estimate of the population total and its standard error
required a modification that is discussed in Appendix B.
be the fractional sample size calculated. Then, if the
fractional part of ui is between 0
and 0.25, it is rounded to 0; between 0.25 and 0.75, to .5;
and between 0.75 and 1.00, to 1. Using this rule, the
estimate of the population total and its standard error
required a modification that is discussed in Appendix B.
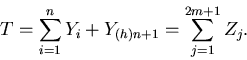
![\begin{eqnarray*}E\left(Y_1 - \frac{2T}{2m+1}\right)^2 & = & E\left[Z_1 + Z_2 - ...
...m+1}_{j=1} Z_j\right]^2 \\
& = & \frac{2(2m-1)}{2m+1} \sigma^2.
\end{eqnarray*}](par.img24.gif)