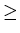 10, the chi-square distribution
with 1 degree of freedom provides a reasonable
approximation to the multinomial probability associated
with the McNemar test statistic,
10, the chi-square distribution
with 1 degree of freedom provides a reasonable
approximation to the multinomial probability associated
with the McNemar test statistic,Joel R. Levin and Ronald C. Serlin
University of Wisconsin - Madison
Journal of Statistics Education v.8, n.2 (2000)
Copyright (c) 2000 by Joel R. Levin and Ronald C. Serlin, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the authors and advance notification of the editor.
Key Words: Correlated proportions; Multinomial proportions; Teaching statistics.
An alternative perspective is presented for teaching students the logic and details underlying McNemar's test of the equality of correlated proportions. The new perspective enables straightforward extension to other correlated proportions situations.
1 It should come as no great revelation to teachers of
introductory applied statistics courses that often students
do not see the conceptual forest for the computational
trees. In a previous article (Serlin and
Levin 1996), we described a forest-seeking method that
capitalizes on the more-intuitive binomial probability
formula to elucidate the less-intuitive hypergeometric
probability formula. A trick used for doing that was
simply to encourage students to view the conventionally
presented
2 In most beginning social-sciences statistics courses, standard hypothesis-testing fare includes the one-, two-, and correlated-sample tests of means, along with the one- and two-sample tests of proportions. Conspicuously absent from this list is McNemar's test of correlated proportions, often referred to as McNemar's test of "change." More properly, however, the procedure represents a test of symmetrical change among those cases in which change actually occurred. Alternatively, and as will be illustrated here, the procedure can be conceptualized as a test of the equality of correlated proportions, even in "nonchange" situations.
3 Of what utility is such a statistical test? Researchers often employ dichotomous dependent variables in a pretest-posttest design to evaluate change or in a matched-pair design to assess the effectiveness of an intervention. Examples of common dichotomous variables of interest include yes-no attitude items and criterion-referenced measures or right-wrong items on a performance test. Of course, from dichotomous variables spring proportions, and just as it is of interest to measure change in mean performance over time, it is frequently of interest to assess changes in proportions (or percentages) over time. For instance, one might wish to document the percentage of prospective voters who change their views of a particular presidential candidate from February to November or the percentage of respondents who become more supportive of a controversial piece of proposed legislation following a statewide media blitz. In a nonrepeated-measures research context, one may wish to compare the performance of specially instructed participants with their matched-pair control counterparts on a dichotomously scored item or on a pass-fail mastery test. In that regard, it should be noted that in situations where matching has been employed, comparing the proportions of "successful" instructed and uninstructed participants via a two-sample chi-square test of homogeneity is not statistically appropriate -- just as an independent samples t test would not be appropriate for assessing a difference in means between the two matched samples.
4 With a single sample and a two-period study as an
example, the data are typically arrayed in a
| H0: pi· = p·i | (1) |
Table 1. Table Representing a One-Sample Correlated Proportions Problem
| Time 2 | ||||
| Correct | Incorrect | Time 1 Totals | ||
| Time 1 | Correct | n11 | n12 | n1· |
| Incorrect | n21 | n22 | n2· | |
| Time 2 Totals | n·1 | n·2 | n·· | |
5 With respect to Table 1, let the
effective sample size be N' = n12
+ n21, the number of observations in the
two "change" cells. For N' 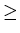 10, the chi-square distribution
with 1 degree of freedom provides a reasonable
approximation to the multinomial probability associated
with the McNemar test statistic,
10, the chi-square distribution
with 1 degree of freedom provides a reasonable
approximation to the multinomial probability associated
with the McNemar test statistic,
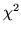 = (n12 - n21)2/(n12 + n21).
= (n12 - n21)2/(n12 + n21).
(A continuity correction, reflected in the numerator as (|n12 - n21| - 1)2, could be included to improve the approximation.) If this test statistic exceeds the alpha-level critical chi-square value, then it is concluded that the two marginal probabilities, pi· and p·i, are not equal, or in the case of Table 1, that the probability of solving the problem correctly is not the same on the two occasions.
6 In introductory social-science statistics texts that cover McNemar's test -- and many do not! -- the test is typically described in terms of the just-presented form of the test statistic (see, for example, Ferguson and Takane 1989, pp. 200-202; Glass and Hopkins 1996, pp. 339-340; and Hays 1994, pp. 865-866). From a pedagogical standpoint, that form of the test essentially comes "out of nowhere" and without a development that allows students to relate it to previously learned tests, such as the Pearson goodness-of-fit chi-square test.
7 For the
This restated null hypothesis allows us to shift our
focus from the margins of the table to just the two change
cells. With attention restricted to those cells and with
equal change cell probabilities specified under the null
hypothesis, the N' observations in the change cells
are equally likely to fall into one or the other change
cell. Accordingly, n12 follows a
binomial distribution with sample size N' and
probability parameter p = 0.5. For N' <
10, the binomial test will provide valid significance
probabilities. For N' 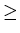 10, students are reminded that
the one-sample test of proportions, H0:
p = 0.5, can be conducted either as a normal
distribution z test or as its squared equivalent, a
one-degree-of-freedom chi-square goodness-of-fit test. (It
can readily be shown that a statistical test that focuses
on just the "change" cells is identical to a test of the
equality of the corresponding multinomial proportions based
on the entire table.) For the chi-square case, the test is
presented in terms of the familiar "observed" (O)
and "expected" (E) cell frequencies as applied to a
2 × 1 table consisting only of the two change cell
frequencies (n12 and
n21 in Table 1).
The goodness-of-fit test yields a value that is
identical to that of the conventional McNemar test.
10, students are reminded that
the one-sample test of proportions, H0:
p = 0.5, can be conducted either as a normal
distribution z test or as its squared equivalent, a
one-degree-of-freedom chi-square goodness-of-fit test. (It
can readily be shown that a statistical test that focuses
on just the "change" cells is identical to a test of the
equality of the corresponding multinomial proportions based
on the entire table.) For the chi-square case, the test is
presented in terms of the familiar "observed" (O)
and "expected" (E) cell frequencies as applied to a
2 × 1 table consisting only of the two change cell
frequencies (n12 and
n21 in Table 1).
The goodness-of-fit test yields a value that is
identical to that of the conventional McNemar test.
8 We now illustrate both the conventional and alternative versions of McNemar's test through actual data that were collected in the first author's introductory educational statistics course, based on a total of 186 students over five semesters. The example provides an underused hypothesis-testing application of McNemar's test, namely, assessing the equality of two proportions associated with two different dichotomous variables at the same point in time. For instance, one might wish to determine whether the proportions of respondents who agree with two different questionnaire items are the same, or whether two items on a test are of equal difficulty, as reflected by the proportion of test takers who get each item correct. In terms of the Table 1 layout, if the focus were on only a single test occasion (e.g., the first test) and the "Time" label were permuted to read "Item," one might wish to determine whether two different items are of equal difficulty.
9 As adapted to our statistics-course example, on the first day of class students are given a 10-item "arithmetic quiz" (essentially a simple algebra test) to assess their readiness for the course. The test consists of five pairs of items, with the items in each pair tapping the same underlying mathematical operation (i.e., the items comprising each pair are structurally equivalent) but presented in one of two different formats: symbolic or verbal. For instance, for one pair of items, the typical symbolically presented format is "Solve for p: 3/5 = p/250." The corresponding verbal format for the same problem is "About two people in five across the country read Time magazine. How many people would we expect to read Time in a random sample of 200 people?" Thus, the second format includes exactly the same underlying structure and required solution operations as the first, but it is presented in a verbal context rather than symbolically. Each problem and its paired counterpart are randomly interspersed throughout the test, with separate total scores calculated for the symbolically and verbally presented problems.
10 In addition to the face value of assessing students'
entering mathematical skill as a predictor of their
success in the course, the algebra test is used to
illustrate a variety of principles related to hypothesis
formulation, research design, and statistical inference.
For instance, an intuitively understandable hypothesis
relates to students' often-reported states of "statistics
anxiety" and "symbol shock": Although most students possess
the prerequisite mathematical problem-solving skills for
the course, they will not demonstrate them as well on
algebra questions presented in less familiar, more
anxiety-producing terms (symbolic) as they will on
questions presented in more familiar everyday contexts
(verbal). If "mastery" is defined as correctly answering
all five problems of a particular format (symbolic or
verbal), one could ask: Do beginning statistics students
demonstrate equivalent mastery of verbally and symbolically
stated algebra problems? The results are summarized in Table 2. Applying the conventional
McNemar formula yields 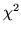 = (31 - 33)2/(31 + 33) =
0.06
= (31 - 33)2/(31 + 33) =
0.06
Table 2. Number of Students Demonstrating Mastery of a Set of Verbally and Symbolically Presented Algebra Problems
| Verbal Format | ||||
| Mastery | Nonmastery | Symbolic Totals | ||
| Symbolic Format | Mastery | 74 | 31 | 105 |
| Nonmastery | 33 | 48 | 81 | |
| Verbal Totals | 107 | 79 | 186 | |
NOTE: Extracted "change" cells are indicated in bold.
11 In contrast, with the alternative perspective, the
data from the present example are recast into the 2 ×
1 table in Table 3, based on just the
N' = 64 students who exhibited a difference in
mastery for the two problem formats. With
O1 = n12 = 31,
O2 = n21 = 33, and
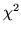 = [(31 - 32)2/32] + [(33 -
32)2/32] = 0.03 + 0.03 = 0.06
= [(31 - 32)2/32] + [(33 -
32)2/32] = 0.03 + 0.03 = 0.06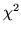 =
[(n12 -
N'/2)2]/(N'/4)
=
[(n12 -
N'/2)2]/(N'/4)
Table 3. "Change" Cells Extracted From Table 2
| Symbolic Format/Verbal Format | Frequency |
| Mastery/Nonmastery | 31 |
| Nonmastery/Mastery | 33 |
12 So what difference does it make which of these two
formulas and associated perspectives is adopted?
Pedagogically, we strongly recommend the latter, primarily
because it: (1) maps directly onto students' previously
acquired binomial, chi-square contingency table, and
goodness-of-fit test concepts; (2) provides consistency and
continuity in extending the one-sample correlated
proportions test to additional applications (as is
demonstrated in
13 It is not uncommon in repeated-measures studies with
dichotomous dependent variables for the researcher to
obtain data from two or more samples. For example, one of
the samples could be a control group and the other(s)
treatment groups. In such experiments, interest focuses on
the equality of the individual McNemar change parameters.
Let k (k = 1, ..., K) denote an
individual's group, and let
pi·k and
p·ik denote the marginal
probabilities of interest in the kth
group. If, in the kth group, the
difference in corresponding marginal probabilities (the
change parameter) is denoted 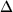 ik =
pi·k -
p·ik, then the null
hypothesis of interest in the multiple-group design,
expressing the equality of the change parameters, is
ik =
pi·k -
p·ik, then the null
hypothesis of interest in the multiple-group design,
expressing the equality of the change parameters, is
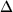 i1 =
··· =
i1 =
··· = 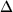 iK
iK
14 In the two-sample case, (1) the number of observations falling into each sample's change cells is unknown prior to the experiment; and (2) in each of the populations from which the samples came, the extent to which the change parameter differs from zero is given by the relative probability of falling into one of the two change cells. Thus, comparing change parameters involves determining whether the relative probability of falling into one of the change cells is independent of group membership, when neither of the margins is fixed. That is, it involves a test of independence, and the appropriate test is the Fisher-Irwin (or "Fisher exact") test.
15 To illustrate the various tests for the two-sample case, consider Table 4, in which some of the Table 2 data are re-presented. Students taking the algebra test are also asked to think back to the college entrance examination that they took in high school and to indicate which of their two subtest scores was higher, verbal or quantitative. Another intuitively interesting hypothesis is that students' differences in mastery of the two problem formats (verbal vs. symbolic) is related to students' verbal vs. quantitative skill profiles. Of the 186 students taking the algebra test, 105 reported higher verbal than quantitative performance on their college entrance examination, 63 reported higher quantitative than verbal, and 18 either did not take such an examination or could not remember their relative performances. The joint frequency data for the 168 students who could be classified as either "higher verbal" or "higher quantitative" are summarized in Table 4.
Table 4. Number of Higher Verbal Students and Higher Quantitative Students Demonstrating Mastery of a Set of Verbally and Symbolically Presented Algebra Problems
| Higher Verbal Students Verbal Format |
Higher Quantitative Students Verbal Format |
||||
| Mastery | Nonmastery | Mastery | Nonmastery | ||
| Symbolic Format | Mastery | 34 | 13 | 38 | 17 |
| Nonmastery | 21 | 37 | 5 | 3 | |
NOTE: Extracted "change" cells are indicated in bold.
16 Consistent with the alternative approach that was
discussed for the one-sample case, the change-cell data are
extracted and compiled into a separate 2
(verbal/quantitative profiles) × 2 (format
combinations) table -- see Table 5. The key here is to
recognize that only the two change cells from each group
are material in assessing the hypothesis of comparable
change symmetry. Because the margins for the newly
constructed
Table 5. "Change" Cells Extracted From Table 4
| Symbolic Format/Verbal Format | Higher Verbal Students | Higher Quantitative Students |
| Mastery/Nonmastery | 13 | 17 |
| Nonmastery/Mastery | 21 | 5 |
17 Alternatively, with large expected "change" cell
frequencies, the traditional Pearson chi-square test of
independence may be used as a convenient approximation.
Additional large-sample approximate procedures include the
likelihood ratio 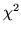 test,
a test based on multinomial proportions (Marascuilo and Serlin 1979), a
test using log-odds ratios (Marascuilo and Serlin 1988, pp.
710-713), and the test of Bishop,
Fienberg, and Holland (1975). For the data in
test,
a test based on multinomial proportions (Marascuilo and Serlin 1979), a
test using log-odds ratios (Marascuilo and Serlin 1988, pp.
710-713), and the test of Bishop,
Fienberg, and Holland (1975). For the data in 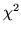 (based on the
familiar
(based on the
familiar
18 Extension to the K > 2 group situation is straightforward, as we illustrate by extending the present example. It may be recalled that 18 students could not be classified as scoring higher on either the verbal or quantitative portion of their college entrance examination. With these students included as an "unknown" third category, the frequency outcomes are summarized in Table 6 (complete data) and Table 7 ("change" cells).
Table 6. Number of Higher Verbal, Higher Quantitative, and Unknown Students Demonstrating Mastery of a Set of Verbally and Symbolically Presented Algebra Problems
| Higher Verbal Students Verbal Format |
Higher Quantitative Students Verbal Format | Unknown Verbal Format |
|||||
| Mastery | Nonmastery | Mastery | Nonmastery | Mastery | Nonmastery | ||
| Symbolic Format | Mastery | 34 | 13 | 38 | 17 | 2 | 1 |
| Nonmastery | 21 | 37 | 5 | 3 | 7 | 8 | |
NOTE: Extracted "change" cells are indicated in bold.
Table 7. "Change" Cells Extracted From Table 6
| Symbolic Format/Verbal Format | Higher Verbal Students | Higher Quantitative Students | Unknown |
| Mastery/Nonmastery | 13 | 17 | 1 |
| Nonmastery/Mastery | 21 | 5 | 7 |
19 For the data in Table 7, a
Pearson chi-square test of homogeneity yields 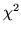 = 12.88 based on 2 degrees
of freedom, with an associated significance probability of
.0016. Because the expected cell frequencies associated
with the unknown category are less than 5, an extension of
the Fisher exact test was also conducted using the computer
program developed by Klotz and Teng
(1975) and yielded a significance probability of
.001.
= 12.88 based on 2 degrees
of freedom, with an associated significance probability of
.0016. Because the expected cell frequencies associated
with the unknown category are less than 5, an extension of
the Fisher exact test was also conducted using the computer
program developed by Klotz and Teng
(1975) and yielded a significance probability of
.001.
20 Familywise 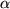 -controlled planned
post-omnibus between-group statistical comparisons of
proportions (e.g., Marascuilo and
Serlin 1988) can be conducted in the
two-degree-of-freedom situation with the Fisher LSD
procedure (Levin, Serlin, and Seaman
1994), as applied to either z or chi-square
statistics or to Fisher exact comparisons, depending on
sample size. For the present three-group example, Fisher's
LSD procedure combined with Fisher exact comparisons (based
on a familywise
-controlled planned
post-omnibus between-group statistical comparisons of
proportions (e.g., Marascuilo and
Serlin 1988) can be conducted in the
two-degree-of-freedom situation with the Fisher LSD
procedure (Levin, Serlin, and Seaman
1994), as applied to either z or chi-square
statistics or to Fisher exact comparisons, depending on
sample size. For the present three-group example, Fisher's
LSD procedure combined with Fisher exact comparisons (based
on a familywise 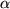 of .05) indicate that
there is a difference in the problem-format outcomes of
higher quantitative students (symbolic format = 55/63
students, or 87%; verbal format = 43/63, or 68%, for a
symbolic-verbal difference of 19%) and both higher verbal
students, as in the two-sample case (47/105 = 45% and
55/105 = 52%, respectively, difference = -7%) and unknown
students (3/18 = 17% and 9/18 = 50%, respectively,
difference = -33%).
of .05) indicate that
there is a difference in the problem-format outcomes of
higher quantitative students (symbolic format = 55/63
students, or 87%; verbal format = 43/63, or 68%, for a
symbolic-verbal difference of 19%) and both higher verbal
students, as in the two-sample case (47/105 = 45% and
55/105 = 52%, respectively, difference = -7%) and unknown
students (3/18 = 17% and 9/18 = 50%, respectively,
difference = -33%).
21 As an interpretive comment, students in the statistics course are alerted to the possibility that numerous demographic and experiential factors in addition to (or other than) the posited mathematics anxiety or relative verbal and quantitative skills could readily contribute to the results, including those related to students' native language, gender, and the like. For example, foreign students in the class may have had a more difficult time comprehending or interpreting the verbally stated questions than the symbolically stated ones simply because of their English language limitations.
22 For more than two-degree-of-freedom situations, other
familywise 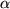 -controlled
multiple-comparison procedures may be employed (Levin et al. 1994). In addition, (1)
Klotz and Teng's (1975) program can be
used to perform exact tests of planned or post hoc, simple
or complex, contrasts among the change-cell proportions;
and (2) when applied to specified contrasts, the approach
introduced here also permits straightforward investigation
of main effects and interactions in multiple-factor
contingency tables.
-controlled
multiple-comparison procedures may be employed (Levin et al. 1994). In addition, (1)
Klotz and Teng's (1975) program can be
used to perform exact tests of planned or post hoc, simple
or complex, contrasts among the change-cell proportions;
and (2) when applied to specified contrasts, the approach
introduced here also permits straightforward investigation
of main effects and interactions in multiple-factor
contingency tables.
23 In this note we have introduced a comprehension-enhancing alternative perspective for the McNemar test of change -- or, more precisely, the multinomial test of correlated proportions. The present perspective allows for direct extensions to two or more samples in which questions of comparable marginal outcome probabilities are of interest. Of additional note is that the present McNemar simplification maps directly onto analogous ones that students can be taught in the context of one-, two-, and K-sample tests of correlated means based on t and F distributions. Comparing two or more different treatments in terms of pretest-posttest differences, as a simplification of the K × 2 split-plot ANOVA treatment by time interaction, is but one example of such mapping (e.g., Levin and Marascuilo 1977). Indeed, one-sample, two-sample, and three-sample correlated t and F tests applied to students' actual verbal and symbolic test scores in the present example (rather than dichotomized "mastery" outcomes) produced statistical conclusions consistent with those already discussed.
Both authors contributed equally to this note. The constructive feedback provided by three anonymous reviewers of an earlier version of the manuscript was appreciated and incorporated.
Bishop, Y. M. M., Fienberg, S. E., and Holland, P. W. (1975), Discrete Multivariate Analysis: Theory and Practice, Cambridge, MA: MIT Press.
Derry, S., Levin, J. R., and Schauble, L. (1995), "Stimulating Statistical Thinking Through Situated Simulations," Teaching of Psychology, 22, 51-57.
Ferguson, G. A., and Takane, Y.
(1989), Statistical Analysis in Psychology and
Education
Glass, G. V., and Hopkins, K. D. (1996), Statistical Methods in Education and Psychology (3rd ed.), Needham Heights, MA: Allyn and Bacon.
Hays, W. L. (1994), Statistics (5th ed.), Orlando: Harcourt Brace.
Klotz, J. H., and Teng, J. (1975), "One-Way Layout for Counts and the Exact H Test With Ties," Technical Report 407, University of Wisconsin - Madison, Department of Statistics.
Lajoie, S. P. (ed.) (1998), Reflections on Statistics: Learning, Teaching, and Assessment in Grades K-12, Mahwah, NJ: Erlbaum.
Levin, J. R., and Marascuilo, L. A. (1977), "Post Hoc Analysis of Repeated Measures Interactions and Gain Scores: Whither the Inconsistency?," Psychological Bulletin, 84, 247-248.
Levin, J. R., Serlin, R. C., and Seaman, M. A. (1994), "A Controlled, Powerful Multiple-Comparison Strategy for Several Situations," Psychological Bulletin, 115, 153-159.
Marascuilo, L. A., and Serlin, R. C. (1979), "Tests and Contrasts for Comparing Change Parameters for a Multiple Sample McNemar Data Model," British Journal of Mathematical and Statistical Psychology, 32, 105-112.
----- (1988), Statistical Methods for the Social and Behavioral Sciences, New York: Freeman.
McNemar, Q. (1947), "Note on the Sampling Error of the Difference Between Correlated Proportions or Percentages," Psychometrika, 12, 153-157.
Serlin, R. C., and Levin, J. R. (1996), "Two Alternative Developments of the Hypergeometric Formula: Turning the Tables," Journal of Statistics Education, [Online], 4(2). (https://www.amstat.org/v4n2/serlin.html)
Joel R. Levin jrlevin@facstaff.wisc.edu
Ronald C. Serlin rcserlin@facstaff.wisc.edu
Department of Educational Psychology
1025 W. Johnson St.
University of Wisconsin
Madison, WI 53706
JSE Homepage | Subscription Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications