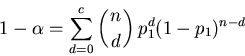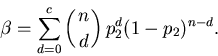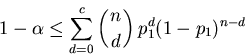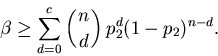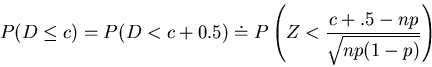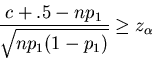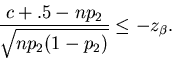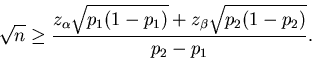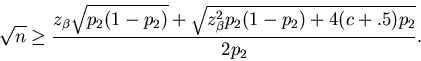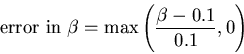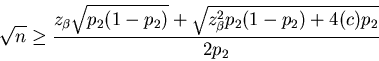Journal of Statistics Education, V8N2:Braun
Replacing a 'Striped-Box' with the Normal Approximation
W. John Braun
University of Western Ontario
Journal of Statistics Education v.8, n.2 (2000)
Copyright (c) 2000 by W. John Braun, all rights
reserved. This text may be freely shared among individuals,
but it may not be republished in any medium without express
written consent from the author and advance notification of
the editor.
Key Words: Acceptance sampling;
Binomial nomograph; Single-sampling plan.
Abstract
A simple procedure is presented for obtaining the
sample size and acceptance number for a single sample
acceptance sampling plan, given the probability of lot
acceptance for lots having proportion defective equal to
p1, and the probability of lot rejection
for lots having proportion defective equal to
p2. The procedure gives a practical
illustration of the use of the normal approximation to the
binomial distribution that is appropriate for courses on
statistical quality control as well as on introductory
statistics.
1. Introduction
1 The most basic acceptance sampling plan considered in
courses on statistical quality control can be described as
follows. A large lot of items is to be inspected in order
to ascertain its quality. A random sample of n
items is selected, and D, the number of defectives
(or nonconforming items) in the sample is counted. If
D exceeds c, the acceptance number, then the
lot is rejected. Otherwise, it is accepted. This is the
so-called single-sampling plan.
2 Because of the simplicity and practicality of such
plans, they are also appropriate for discussion or
exercises in introductory courses on statistics, especially
those designed for mathematics or statistics majors. They
are useful as examples of binomial and hypergeometric
models. In addition, the designing of such plans (that is,
deciding upon n and c) provides nice
nontrivial examples of the use of the normal approximation
to the binomial distribution, highlighting the importance
of the continuity correction, which is often one of the
more difficult topics to motivate in an introductory
course. Strangely, the approach taken toward designing
such plans described in popular quality control textbooks
avoids mention of the normal approximation to the binomial,
even if the approximation is described in the 'statistical
background' chapter. Instead, a 'black-box' method based on
something called a binomial nomograph is described (see,
e.g., Montgomery 1996), and an
opportunity to demonstrate the normal approximation in a
practical setting is missed.
3 Such plans are usually designed (that is, n and
c are chosen) to satisfy the competing interests
of the lot producer and the lot consumer. The lot producer
would like the probability of lot acceptance (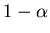 )
to be high when the proportion of nonconforming units
(p1) is low. The consumer requires the
probability of lot acceptance (
)
to be high when the proportion of nonconforming units
(p1) is low. The consumer requires the
probability of lot acceptance (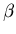 )
to be low when the proportion of nonconforming units
(p2) is high. In the quality control
textbook by Montgomery (1996, p.
620), it is stated that n and c should be
taken to satisfy
)
to be low when the proportion of nonconforming units
(p2) is high. In the quality control
textbook by Montgomery (1996, p.
620), it is stated that n and c should be
taken to satisfy
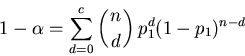 |
(1) |
and
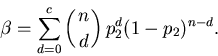 |
(2) |
Montgomery goes on to say that
the nonlinear equations (1) and
(2) have no simple, direct solution. A binomial
nomograph is then exhibited for use in obtaining solutions
to these equations. The nomograph is a nonregular grid
for which a relatively simple, but apparently magical, set
of rules can be followed to obtain n and c,
for given 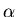 ,
,
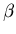 ,
p1, and p2. An
equivalently magical procedure is provided by Mitra (1998, p. 438-441), in which case a
table of Grubbs (1949) has been used
to obtain sampling plans.
,
p1, and p2. An
equivalently magical procedure is provided by Mitra (1998, p. 438-441), in which case a
table of Grubbs (1949) has been used
to obtain sampling plans.
 Figure 1 (123.2K jpg)
Figure 1 (123.2K jpg)
Figure 1. A Binomial Nomograph from Montgomery (1996, p. 620) (used
with permission).
4 The goal of the present note is to make some remarks
about the above equations and procedure and to present an
alternative, simpler procedure for designing
single-sampling plans. The idea is that the normal
approximation to the binomial distribution leads to
approximations for n and c, given 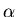 and
and 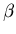 .
A key motivation is to replace the black-box nature of the
above nomograph procedure with a procedure that can be
relatively easily understood. Such a procedure could be
demonstrated in either an introductory statistics course or
in a quality control course.
.
A key motivation is to replace the black-box nature of the
above nomograph procedure with a procedure that can be
relatively easily understood. Such a procedure could be
demonstrated in either an introductory statistics course or
in a quality control course.
2. Some Remarks and the Normal Approximation Solution
5 The first thing to observe is that the nonlinear
equations will usually not have an integer-valued
solution. Thus, the nomograph will not usually provide a
true solution, but it will yield an approximate solution.
This will be accomplished by choosing the nearest grid
point on the nomograph to the real-valued solution that the
nomograph provides. One problem with this technique is
that the resulting sampling design may sometimes result in
probabilities of acceptance that are too low at
p1 and/or too high at
p2. What is really sought is a sampling
design that satisfies (or comes close to satisfying) the
inequalities
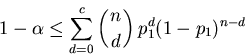 |
(3) |
and
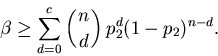 |
(4) |
Usually, one would want to use the smallest value of
n satisfying both inequalities. Using the normal
approximation to the binomial distribution with the
continuity correction, we have
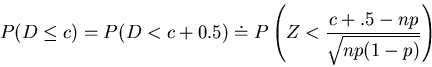 |
(5) |
where Z is a standard normal random variable.
Thus, inequality (3) implies
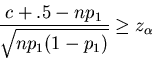 |
(6) |
where
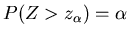 ,
and inequality (4) implies
,
and inequality (4) implies
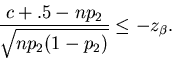 |
(7) |
Thus,
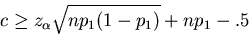 |
(8) |
and
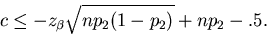 |
(9) |
A quadratic inequality in 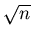 can then be obtained by subtracting the first inequality
from the second. The relevant solution satisfies
can then be obtained by subtracting the first inequality
from the second. The relevant solution satisfies
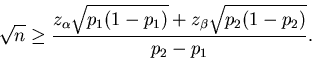 |
(10) |
One possible value of n to try is the smallest
integer satisfying the above inequality. The value of
c may then be chosen as the smallest integer
satisfying (8). However, the
previously chosen value of n may not satisfy (9) for this particular value of
c, so the value of n may need to be revised
accordingly. This time, (9) may be
viewed as a quadratic inequality in 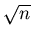 ,
and the relevant solution set is given by
,
and the relevant solution set is given by
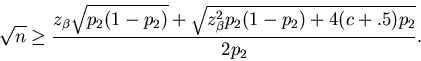 |
(11) |
The value of n should then be taken as the
smallest integer satisfying (11). In some circumstances, one
may wish to revise c, using the newly revised value
of n and inequality (8),
but this is usually not necessary.
6 Table 1 gives an indication of
the quality of the sampling plans obtained using the normal
approximation (with continuity correction) for some
typical situations. The nominal values of 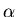 ,
,
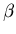 ,
and p1 are fixed at .05, .1, and .01,
respectively. The table provides the sampling plans for
the tabulated values of p2, and also
gives the true binomial probabilities
,
and p1 are fixed at .05, .1, and .01,
respectively. The table provides the sampling plans for
the tabulated values of p2, and also
gives the true binomial probabilities
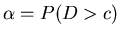 (at p1) and
(at p1) and
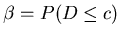 (at p2). These are listed in the fourth
and fifth columns, respectively.
(at p2). These are listed in the fourth
and fifth columns, respectively.
Table 1. Some Continuity Corrected
Single-Sampling Plans for Various Values of
p2, With p1 =
0.01,
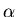 = 0.05 (Nominal), and
= 0.05 (Nominal), and
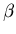 = 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
= 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
| p2 |
n |
c |
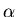 |
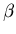 |
error in 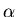 |
error in 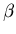 |
| 0.020 |
1184 |
17 |
0.0561 |
0.0952 |
0.122 |
0 |
| 0.025 |
620 |
10 |
0.0505 |
0.0933 |
0.011 |
0 |
| 0.030 |
395 |
7 |
0.0473 |
0.0929 |
0 |
0 |
| 0.035 |
268 |
5 |
0.0542 |
0.0905 |
0.084 |
0 |
| 0.040 |
202 |
4 |
0.0536 |
0.0906 |
0.071 |
0 |
| 0.045 |
179 |
4 |
0.0349 |
0.0914 |
0 |
0 |
| 0.050 |
135 |
3 |
0.0474 |
0.0901 |
0 |
0 |
| 0.060 |
90 |
2 |
0.0619 |
0.0880 |
0.239 |
0 |
| 0.070 |
77 |
2 |
0.0424 |
0.0875 |
0 |
0 |
| 0.080 |
67 |
2 |
0.0298 |
0.0882 |
0 |
0 |
| 0.090 |
60 |
2 |
0.0224 |
0.0846 |
0 |
0 |
| 0.100 |
40 |
1 |
0.0607 |
0.0805 |
0.215 |
0 |
| 0.120 |
33 |
1 |
0.0430 |
0.0810 |
0 |
0 |
| 0.150 |
26 |
1 |
0.0277 |
0.0817 |
0 |
0 |
NOTE: The relative error in the constraints (3) and (4) is indicated in the last
two columns.
7 It should be noted that, because the normal
approximation is used, the required inequalities are
sometimes mildly violated, especially (3); however, the violations are
usually no worse than those for the Grubbs' table or the
nomograph. The sixth and seventh columns of Table 1 indicates the relative size of
these errors. That is,
and
8 The method is surprisingly accurate even for cases
where n turns out to have a small value. This is
consistent with observations made by Kupper and Hafner (1989) about finding
sample sizes for hypothesis tests when both test size and
power at a particular alternative are specified.
3. Discussion
9 In practice, one could check
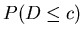 for both values of p to ensure that the sampling
plan is satisfactory. If it is not, one could experiment
with slightly larger values of n (together with the
corresponding c values) to obtain plans that
conform more closely to the nominal values of
for both values of p to ensure that the sampling
plan is satisfactory. If it is not, one could experiment
with slightly larger values of n (together with the
corresponding c values) to obtain plans that
conform more closely to the nominal values of
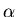 and
and 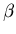 .
.
10 It is also possible to try to correct the
approximation using Cornish-Fisher expansions (e.g.,
Hall 1992). For example,
one can show that
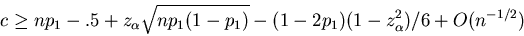 |
(12) |
and
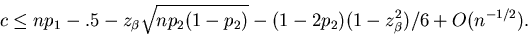 |
(13) |
Then, a sampling plan can be obtained by solving another
quadratic inequality for 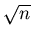 .
The resulting plans obey inequalities (3) and (4) more often than the
uncorrected plans. Table 2 lists the
corrected plans that correspond to the ones in Table 1, together with the actual
probabilities of rejection at p1 and
acceptance at p2. Although not listed in
the table, there are some plans found by this procedure
that violate inequality (3).
.
The resulting plans obey inequalities (3) and (4) more often than the
uncorrected plans. Table 2 lists the
corrected plans that correspond to the ones in Table 1, together with the actual
probabilities of rejection at p1 and
acceptance at p2. Although not listed in
the table, there are some plans found by this procedure
that violate inequality (3).
Table 2. Cornish-Fisher Corrected
Single-Sampling Plans for Various Values of
p2, With p1 = 0.01,
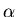 = 0.05 (Nominal), and
= 0.05 (Nominal), and
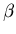 = 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
= 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
| p2 |
n |
c |
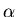 |
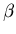 |
error in 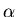 |
error in 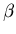 |
| 0.020 |
1236 |
18 |
0.0466 |
0.0989 |
0 |
0 |
| 0.025 |
615 |
10 |
0.0483 |
0.0985 |
0 |
0 |
| 0.030 |
391 |
7 |
0.0451 |
0.0985 |
0 |
0 |
| 0.035 |
300 |
6 |
0.0328 |
0.0976 |
0 |
0 |
| 0.040 |
231 |
5 |
0.0298 |
0.0972 |
0 |
0 |
| 0.045 |
177 |
4 |
0.0335 |
0.0964 |
0 |
0 |
| 0.050 |
133 |
3 |
0.0453 |
0.0961 |
0 |
0 |
| 0.060 |
110 |
3 |
0.0250 |
0.0980 |
0 |
0 |
| 0.070 |
75 |
2 |
0.0397 |
0.0968 |
0 |
0 |
| 0.080 |
66 |
2 |
0.0287 |
0.0935 |
0 |
0 |
| 0.090 |
58 |
2 |
0.0205 |
0.0965 |
0 |
0 |
| 0.100 |
52 |
2 |
0.0154 |
0.0966 |
0 |
0 |
| 0.120 |
43 |
2 |
0.0092 |
0.0970 |
0 |
0 |
| 0.150 |
25 |
1 |
0.0258 |
0.0931 |
0 |
0 |
NOTE: The relative error in the constraints (3) and (4) is indicated in the last
two columns.
11 One might argue that when using the Cornish-Fisher
correction, the simplicity and directness of the method
are sacrificed. For most practical purposes, the normal
approximation is probably adequate, and it is certainly
easier for an undergraduate student to understand. On the
other hand, it might not hurt for a senior undergraduate to
see that there are relatively simple ways to improve on the
normal approximation.
12 The continuity correction itself seems to be necessary
in order to provide accurate results. If the correction is
ignored, the above inequalities are violated fairly often,
and sometimes by a substantial margin, as can be seen from
Table 3. That table corresponds
exactly to Table 1, except that
is used in place of (8) and
is used in place of (11).
Inequality (10) is still used to
obtain the initial estimate of n.
Table 3. Uncorrected
Single-Sampling Plans for Various Values of
p2, With p1 = 0.01,
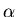 = 0.05 (Nominal), and
= 0.05 (Nominal), and
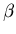 = 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
= 0.1 (Nominal), Together With Actual
Probabilities of Lot Rejection (at p1)
and Acceptance (at p2)
| p2 |
n |
c |
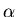 |
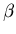 |
error in 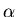 |
error in 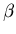 |
| 0.020 |
1213 |
18 |
0.0400 |
0.115 |
0 |
0.155 |
| 0.025 |
596 |
10 |
0.0401 |
0.120 |
0 |
0.203 |
| 0.030 |
375 |
7 |
0.0368 |
0.123 |
0 |
0.240 |
| 0.035 |
286 |
6 |
0.0262 |
0.125 |
0 |
0.251 |
| 0.040 |
218 |
5 |
0.0233 |
0.128 |
0 |
0.286 |
| 0.045 |
165 |
4 |
0.0258 |
0.131 |
0 |
0.317 |
| 0.050 |
148 |
4 |
0.0170 |
0.132 |
0 |
0.329 |
| 0.060 |
101 |
3 |
0.0189 |
0.137 |
0 |
0.378 |
| 0.070 |
87 |
3 |
0.0115 |
0.133 |
0 |
0.339 |
| 0.080 |
59 |
2 |
0.0214 |
0.139 |
0 |
0.392 |
| 0.090 |
52 |
2 |
0.0153 |
0.141 |
0 |
0.417 |
| 0.100 |
47 |
2 |
0.0116 |
0.138 |
0 |
0.383 |
| 0.120 |
39 |
2 |
0.0069 |
0.137 |
0 |
0.374 |
| 0.150 |
21 |
1 |
0.0185 |
0.155 |
0 |
0.550 |
NOTE: The relative error in the constraints (3) and (4) is indicated in the last
two columns.
13 It should be noted that the nomograph is unable to
provide sampling plans outside a certain range. For
example, if 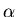 = .001,
= .001,
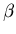 = .1, p1 = .01, and p2
= .02, then the nomograph cannot be used to obtain a plan,
but the normal approximation method gives the sampling
plan: n = 2416 and c = 39 and
= .1, p1 = .01, and p2
= .02, then the nomograph cannot be used to obtain a plan,
but the normal approximation method gives the sampling
plan: n = 2416 and c = 39 and
and
Also, the nomograph will not yield any sampling plans
when p < .01. The Grubbs' table will not
provide any sampling plans where c exceeds 15. The
normal approximation is much more widely applicable.
14 Finally, there is the important pedagogical value of
the above approach. Not only is this a relatively simple
way to replace a black-box (or striped-box) solution, but
it is also a useful application of the normal approximation
to the binomial distribution.
Acknowledgments
The helpful comments and suggestions of three anonymous
referees have led to a substantial improvement in the paper
and are gratefully acknowledged. This work was supported by
a research grant from the Natural Sciences and Engineering
Research Council of Canada (NSERC) and was completed during
a visit to the Centre for Mathematics and Its Applications
at the Australian National University in Canberra,
Australia.
References
Grubbs, F. E. (1949), "On Designing
Single Sampling Plans," Annals of Mathematical
Statistics, 20, 256.
Hall, P. (1992), The Bootstrap and
Edgeworth Expansion, New York: Springer-Verlag.
Kupper, L. L., and Hafner, K. B. (1989),
"How Appropriate Are Popular Sample Size Formulas?"
The American Statistician, 43, 101-105.
Mitra, A. (1998), Fundamentals of
Quality Control and Improvement (2nd ed.), Upper
Saddle River, New Jersey: Prentice Hall.
Montgomery, D. C. (1996),
Introduction to Statistical Quality Control
(3rd ed.), New York: Wiley.
W. John Braun
Department of Statistical and Actuarial Sciences
Western Science Centre
University of Western Ontario
London, Ontario, Canada N6A 5B7
braun@stats.uwo.ca
JSE Homepage | Subscription
Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search
JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications
![]() ,
,
![]() ,
p1, and p2. An
equivalently magical procedure is provided by Mitra (1998, p. 438-441), in which case a
table of Grubbs (1949) has been used
to obtain sampling plans.
,
p1, and p2. An
equivalently magical procedure is provided by Mitra (1998, p. 438-441), in which case a
table of Grubbs (1949) has been used
to obtain sampling plans.