Richard M. Single
St. Michael's College
Journal of Statistics Education v.8, n.1 (2000)
Copyright (c) 2000 by Richard M. Single, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the author and advance notification of the editor.
Key Words: Sampling frame; Stratification; Survey design.
The use of tangible examples can make the concepts of statistical sampling and survey design more meaningful for college students. These concepts are especially relevant with the advent of the 2000 Census and the debate over its use of statistical sampling.
In this paper, basic ideas from survey design are introduced using the 2000 Census as an example, in order to capitalize on the recent media attention. Then, these same concepts are applied to the National Health Interview Survey (NHIS). Data for the 1993 NHIS can be accessed through the National Center for Health Statistics web site and simple analyses can be performed over the web to demonstrate the use of sampling weights. In addition, subsets of the data can be downloaded and analyzed using statistical software packages.
The methods of statistical sampling and the structure of a national survey have a variety of applications in the classroom, depending on the level of the course being taught. This paper discusses some of these applications and how to access and use these data as an effective teaching tool.
1 In this paper, basic ideas from survey design are introduced using the 2000 Census as an example, in order to capitalize on the recent media attention. Then, these same concepts are applied to the National Health Interview Survey (NHIS). The main objective of this paper is to introduce basic information about a major national survey that can be used as an example in the classroom. In addition, two examples are presented that describe how data from the NHIS can be accessed via the Internet. The NHIS, in particular the 1993 survey, was chosen because of its accessibility. It can be used by teachers and students to explore concepts related to survey design, such as sampling and stratification, and issues related to the development and execution of surveys.
2 The 1993 National Health Interview Survey included 52,467 males and 57,204 females. Through the use of statistical weights, these 109,671 individuals represent a population of 254,281,227, which is an approximation of the 1993 noninstitutionalized U.S. population. The NHIS is one of the oldest national health surveys conducted by the U.S. Bureau of the Census for the National Center for Health Statistics (NCHS). Recently, the Census Bureau has received a great deal of attention in politics and the news for its proposed statistical methods in the 2000 Census.
3 This paper discusses issues related to statistical sampling and the use of statistical weights using the NHIS and the 2000 Census. These issues have a variety of illustrative uses in the classroom depending on the level of the course being taught. Sampling and weighting can be mentioned as enrichment topics in an introductory statistics class, can be explored in further detail with intermediate statistics students, and can be used in a project, lab, or an independent study with upper level students.
4 After a brief description of some of the controversy over the 2000 Census in Section 1.2, the concepts of sampling and statistical weights are introduced in Section 1.3 using the 2000 Census as an example. In Section 2, the concepts of sampling design and weights are discussed in relation to the NHIS. Section 3 discusses the availability of NHIS data over the Internet. In Section 4, aspects of using the NHIS as a teaching tool are discussed.
5 There has been much debate over the use of statistical sampling for the 2000 Census. Statistical sampling has been suggested as a way to correct the undercount and differential coverage of U.S. residents. This undercount is more severe for certain minority groups. Table 1 lists estimated percent undercounts from the 1990 Census generated by the Census Bureau from the Post Enumeration Survey.
Table 1. Estimated 1990 Census Net Undercount
| Population | Estimated percent undercount |
| African American | 4.4% |
| Hispanic (all races) | 5.0% |
| American Indian (living on reservations) | 12.2% |
| White (non-Hispanic) | 0.7% |
Source: U.S. Census Bureau (1997), "Report To Congress -- The Plan for Census 2000," http://www.census.gov/main/www/2kplans.html
6 The debate focuses on the use of statistical weights and the assumptions that need to be made in order to incorporate statistical sampling in the census. Because there are many uses for the information collected in the census, these issues have become politicized. In August of 1998, a Federal Court panel determined that an actual head count must be used to allocate congressional seats among the states. The court panel ruled that the use of statistical sampling for the apportionment of congressional seats would be a violation of the Census Act. Arguments against the use of statistical sampling for congressional apportionment claim that manipulation of the sample selection would occur by Republicans and Democrats alike. As Moore (1998) states with regard to the misrepresentation of the scientific method of statistical sampling, there are fears that "a conspiracy lurks behind every weighted mean."
7 In April of 1998, the American Statistical Association (ASA) filed an amicus brief in the census court cases responding to attacks on the methodology of statistical sampling (American Statistical Association 1998, https://www.amstat.org/outreach/amicus.html). The brief stated that the ASA does not take a position on the legality or constitutionality of statistical sampling in the 2000 Census. It went on to state that the "ASA is, however, concerned to defend statistically designed sampling as a valid, important, and generally accepted scientific method for gaining accurate knowledge about widely dispersed human populations."
8 The NHIS and the 2000 Census provide excellent examples to introduce students to statistical weights and sampling. The concept of statistical weights will be introduced below using one of the proposed adjustments for the 2000 Census at a level that is approachable for college-level statistics students.
9 Although statistical sampling will not be used for congressional apportionment, the Census Bureau will use this technique to help increase the accuracy of the 2000 Census for other applications. The Census Bureau has issued two plans for conducting the 2000 Census. The first, "Census 2000 Operational Plan," uses statistical sampling methodology throughout. The second, "Census 2000 Operational Plan: Using Traditional Census-Taking Methods," is a plan for conducting the census without statistical sampling for the purpose of apportionment.
10 Under the first plan, a scientific sample survey of approximately 300,000 housing units will be conducted after the Census enumeration to generate corrected counts (U.S. Census Bureau 1999). For the 2000 Census, this survey is called the Accuracy and Coverage Evaluation (ACE). An estimate of the number of people missed or incorrectly counted in the Census will be made based on the results of the ACE. The "CensusPlus" plan, one of the methods for correcting the counts considered by the Census Bureau, is described below. Although this is not the method chosen by the Census Bureau, it is described in detail because it has an intuitive appeal that makes it accessible to students.
11 Suppose that one wants to determine the number of people, NA, living in an eight block region A. After an initial enumeration is made in this region, a second independent enumeration is made in a randomly chosen subset of region A, say a two-block region B. Extra effort is put into this second enumeration so that a higher proportion of the actual residents are counted.
12 To describe the adjustment of the count in region A based on the second enumeration of subregion B, I will define the following terms:
nij: the number of people found in region i by enumeration j, where i = A, B, and j = 1, 2
nB(12): the number of people found in region B by either the first or the second enumeration
Then, the corrected count for region A, using the "CensusPlus" correction, is
13 It can be pointed out to the students that this is the
original count in region A multiplied by a scaling
factor that is always greater than or equal to one. The
scaling factor, nB(1![]() 2)/
nB1, is the statistical weight
for an individual in region A. Since the numerator
is the number of people found by either enumeration, it is
always greater than or equal to the denominator, which is
the number found in the first enumeration. The statistical
weight is larger when more people are identified by the
second enumeration that were not identified by the first.
Using the "CensusPlus" correction, each individual in
region A represents nB(1
2)/
nB1, is the statistical weight
for an individual in region A. Since the numerator
is the number of people found by either enumeration, it is
always greater than or equal to the denominator, which is
the number found in the first enumeration. The statistical
weight is larger when more people are identified by the
second enumeration that were not identified by the first.
Using the "CensusPlus" correction, each individual in
region A represents nB(1![]() 2)/nB1 people.
2)/nB1 people.
14 The method chosen by the Census Bureau is called Dual System Estimation. The count correction is similar to one based on the capture-recapture method with an added adjustment for the estimated number of erroneous enumerations made in the Census (See Mulry and Griffiths 1996 for details).
15 It is important for students to realize that statistical sampling is used not only as a means of correcting population counts, but can be used as an integral part of a sampling design (Ferber, Sheatsley, Turner, and Waksberg 1980). For example, statistical sampling has been used by the Census Bureau since 1940 to determine which housing units are sent detailed questionnaires. Only 17% of all housing units are slated to receive the "long form," which requests more detailed demographic information from the respondents. The subset of the U.S. population that receives the "long form" instead of the "short form" is determined using a scientific sample to ensure the accuracy and reliability of estimates made from these data.
16 The NHIS is an example of a survey that uses statistical sampling to produce estimates that are representative at a national level. Discussion of the sampling design and the development of statistical weights in the NHIS provides an interesting example that can be used to highlight several topics in survey design and probability.
17 The National Health Interview Survey has been conducted annually since 1957 by the U.S. Bureau of the Census for the NCHS to provide information about the health of the resident, civilian, noninstitutionalized population living at the time of the interview. It is one of the oldest national health surveys. The survey is not administered to individuals living in nursing homes, members of the armed forces, individuals that are institutionalized, or United States citizens living abroad.
18 The survey includes a core set of questions on demographic and health-related variables, which remain relatively constant, and a set of supplements that change from year to year. The core survey is administered to every individual in the sample. Each individual is then asked questions from one of the supplements.
19 The sampling design of the NHIS is a multistage, personal interview probability sample (Massey, Moore, Parsons, and Tadros 1989). The sampling frame consists of geographical areas defined in three stages. Every member of the target population, the resident, civilian, noninstitutionalized U.S. population, belongs to one area unit. This complex design is used so that the resulting data are representative of the target population, a high response rate is maintained, and the cost of executing the survey is not prohibitive.
20 In the first stage of the sampling design, the United States is divided into approximately 1,900 geographic regions called Primary Sampling Units (PSUs). A PSU consists of a county, a group of adjacent counties, or a Metropolitan Statistical Area (MSA) (see Figure 1).
Figure 1. Flowchart of the NHIS Sampling Design.
21 The 52 largest PSUs are automatically selected into the sample. These are called self-representing PSUs. The remaining non-self-representing PSUs are then clustered into 73 strata based on socioeconomic and demographic variables. From each of the 73 strata, two PSUs are selected into the sample with probability proportional to the size of their population. These 146 non-self-representing and 52 self-representing PSUs give a total of 198 PSUs selected in the first stage.
22 In the second stage of the sampling design, the PSUs are divided into smaller geographic units called segments. Each segment consists of several households. Roughly 7,500 segments are sampled from the total number that are identified. In order to improve the precision of estimates for minorities, the NHIS uses a technique known as oversampling.
23 In PSUs with between 5% and 50% minority population, oversampling is incorporated into the survey design by assigning segments to one of two strata according to the proportion of the minority population. In the stratum with high minority concentrations, the sampling rates for segment selection are increased. In the other stratum of the same PSU, the sampling rates are decreased. This is done so that the sample size within each PSU is the same as it would be if oversampling were not used. Oversampling was used in 102 PSUs. According to Census Bureau estimates, the proportion of persons in minority groups, for which oversampling was done, was 16%. If oversampling had not been used, the proportion would have been 11%.
24 In the third stage of the sampling design, the NCHS selects households at which the survey will be administered by one of the 140 interviewers. If there is a manageable number of households in a segment, an interview is attempted at each occupied household within each segment included in the sample. Otherwise, if there is a large number of households in a segment, a sample of households is chosen to be interviewed. The response rate for households that are selected to be in the sample has continually been over 95%. In 1993, the NHIS consisted of 43,007 households containing 109,671 people.
25 Each person included in the sample has a known positive probability of selection for the survey. After the survey is completed, the probability of selection is adjusted (e.g., for nonresponse) to produce the final sampling weights. Using these sampling weights, the data can be used to represent the total United States population. The sampling weight for each person in the sample defines the number of individuals in the population that he or she represents. For the 1993 NHIS sample, the sampling weights are between 230 and 11,694, with the median weight at 2,052.
26 For each person in the sample, a basic statistical weight is made up of three components, corresponding to the three sampling stages. Let pi denote the probability that the ith PSU is selected, pj denote the probability that the jth segment is selected, and pk denote the probability that the kth household is selected. The basic statistical weight, w*ijk, for individuals in the ith PSU, jth segment, and kth household, is defined as
27 Three ratio adjustments are applied to the basic statistical weight in order to adjust for any nonresponse of households within a segment, to help correct any bias due to undercoverage, and to make the sample more closely resemble the age, sex, and race distribution in the population. These ratios are derived from independent data sources by the U.S. Bureau of the Census. The resulting final weight for the ith individual in the survey will be denoted as wi, and is equal to the number of people in the target population represented by the ith individual in the survey.
28 The Federal Electronic Research and Review Extraction Tool (FERRET) provides an interface for accessing data from the NHIS over the Internet. FERRET was developed by the U.S. Bureau of the Census and the Bureau of Labor Statistics. A link to FERRET is located at the NCHS web site http://www.cdc.gov/nchs/datawh/ferret/ferret.htm. Alternatively, the data are available on CD-ROM from the NCHS (National Health Interview Survey 1993).
29 Using FERRET, you can select variables, view or download a codebook for the variables, and download either a SAS or an ASCII dataset. FERRET has a search engine that allows you to identify variables of interest from the NHIS dataset. You can generate cross-tabulations or frequency distributions for the variables that you select over the web and can choose to create these descriptive statistics using statistically weighted or unweighted data.
30 The information in Table 2 was generated from the core survey data located in the "Person file" using FERRET. The "Person file" contains one record for each person for whom data from the core questionnaire was collected in a selected household.
Table 2. Age Specific Weighted and Unweighted Counts from the 1993 NHIS
| Unweighted Counts | Weighted Counts | Age Specific Percent of Weighted Counts |
||||
| Age | Male | Female | Male | Female | Male | Female |
| 0- 4 | 4,512 | 4,188 | 10,193,726 | 9,720,580 | 51.19 | 48.81 |
| 5-17 | 11,185 | 10,627 | 24,334,139 | 23,209,177 | 51.18 | 48.82 |
| 18-24 | 4,785 | 5,010 | 11,895,851 | 12,242,939 | 49.28 | 50.72 |
| 25-44 | 16,259 | 18,244 | 40,200,381 | 41,425,944 | 49.25 | 50.75 |
| 45-64 | 10,251 | 11,177 | 23,951,188 | 25,836,971 | 48.11 | 51.89 |
| 65-69 | 1,917 | 2,478 | 4,509,937 | 5,498,265 | 45.06 | 54.94 |
| 70-74 | 1,619 | 2,109 | 3,849,684 | 4,757,781 | 44.72 | 55.28 |
| 75+ | 1,939 | 3,371 | 4,770,742 | 7,883,922 | 37.70 | 62.30 |
| Total | 52,467 | 57,204 | 123,705,648 | 130,575,579 | 48.65 | 51.35 |
Source: FERRET, http://ferret.bls.census.gov/cgi-bin/ferret
31 A discussion of the three stages of the NHIS sampling design provides examples of sampling frames, target populations, stratification, and sampling. Accessibility via the Internet allows the NHIS to serve as an example and a teaching tool for statistics classes at various levels.
32 One of the best ways to help students understand surveys and sampling is to get them to think about and discuss the issues involved in carrying out a survey. For example, students (or groups of students) can be asked to design a survey that would measure some health-related outcome in the U.S. population. Along with the actual survey questions, they can be asked to consider how they might achieve a nationally representative sample. Each student (or group) can exchange their proposal with another student (or group) to critique their respective plans. Students can assess their classmates' plans for potential bias, under or over representation, and feasibility. This exercise helps students understand what is involved in making a sample representative of a target population, when the target population is large and geographically diverse. In particular, it helps increase students' appreciation of the sampling design issues in the NHIS. Explaining that the NHIS is administered yearly, and that the resulting data are subsequently used for research and health policy, provides some perspective for the students.
33 A discussion about sampling frames can be enhanced by considering the difference between a list frame (an identification, or listing, of elements from the population of interest) and an area frame (an identification of subsets of elements, defined geographically, from the population of interest). As mentioned in Section 2.2, the NHIS uses a sampling frame consisting of geographic areas. It is interesting to note that, although the U.S. Bureau of the Census conducts the NHIS, it does not use a list frame compiled from the list of addresses in the decennial census. The Census Bureau must guarantee the confidentiality of information collected in the decennial census, and, under Title 13 of United States Code, is not allowed to release any identifiable household information to other Federal statistical agencies. Without this identifiable information, it would not be possible for the NCHS to analyze the results of the NHIS in sufficient geographical detail or to conduct follow-up surveys. These are the major reasons why an area sampling frame is used for conducting the NHIS.
34 Stratified sampling is a topic that appears in most introductory courses. The sampling design of the NHIS provides a good example of the use and importance of stratification. In the first stage of the sampling design, the non-self-representing PSUs (those PSUs that are not automatically selected into the sample) are clustered into 73 strata. Then two PSUs are selected from each stratum. Stratifying variables used by the NHIS include poverty status, ethnic origin, urban/non-urban area, and employment status. The choice of stratifying variables is an excellent discussion topic. What makes a variable a good choice as a stratifying variable? If the major concern of the survey were financial issues rather than health issues, how would this affect the choice of stratification variables?
35 Information such as that in Table 2 can be used to introduce or reinforce the idea of sampling weights. In a probability class, the composition of the sampling weights can be used to provide an example of independence in an interesting applied probability setting. In most college statistics courses, students are primarily exposed to equal probability sampling. Because of this, and misrepresentation in the media, students may misinterpret unequal probability sampling as incorrect or "biased" (Overton and Stehman 1995).
36 A discussion of the design issues in the NHIS can be used to emphasize the fact that the probability of selection must be known for each sampled individual in any valid probability sampling design. Also, students can see how the sampling design along with the probability of selection makes it possible for estimates from the data to be representative of the target population. For example, using the data in Table 2, students can investigate the national sex distribution across age groups. In Table 2, the 5,010 females aged 18-24 represent 12,242,939 women in the target population, or 50.72% of those in this age group. Thus, on average, each woman in this age group represents approximately 2,444 women. In other words, the average statistical weight for women in this age group is approximately 2,444.
37 In addition, the NHIS can be used to introduce the
concept of weighted means. For example, suppose that
xi represents the height of the
ith individual in the survey. Then, using
the final statistical weights, an estimate of the average
height of males aged 18-24, ![]() ,
in the target population is given by the following weighted
mean
,
in the target population is given by the following weighted
mean
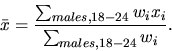
Note that the numerical value of the denominator, 11,895,851, appears in Table 2. Most statistical packages allow the user to specify weights to be used in constructing cross-tabulations and in the calculation of means and totals.
38 In an advanced class or as an independent study, the NHIS can be used to provide context and the data source for investigations of variance estimation in a complex survey. Potential topics include the jackknife estimator of the variance, the use of alternative statistical packages, and the Horvitz-Thompson Theorem for means and variances from probability samples (see Overton and Stehman 1995). Most general purpose statistical packages do not incorporate complex survey design features in their calculation of variances. This typically leads to underestimates of the variances. Software packages such as SUDAAN (Shah, Barnwell, and Bieler 1997) do provide this capability. Results from these packages or printed reports (e.g., Benson and Marano 1994) can be used as a benchmark for these investigations.
39 To facilitate the use of FERRET and the NHIS as a teaching tool, two examples are presented below. The examples begin with a research question. They continue with an explanation of how FERRET can be used to retrieve information from the NHIS that can be used to address the question. The first example involves analyses conducted over the Internet using FERRET. An instructor might generate the output from this example and distribute it to students, or have students generate the output themselves. The second example is for a more advanced audience. It discusses a situation where a dataset is downloaded and imported into a statistical analysis package. An instructor might download the data and distribute it to students or have students download their own data in an advanced class.
40 As a first example, the following question will be considered. Are there regional or gender differences in the amount of salt that young adults add to their food? To extract information from the NHIS, the "Year 2000" supplement is selected from FERRET's Survey Form Page. FERRET then brings the user to the Data Search Page to identify variables of interest. A search of the variable names and descriptions was done for the following terms: age, region, sex, and salt. The variables AGER1 (age recode #1), REGION, SEX, and ADDSALT (how often add salt to food) were then selected from the Select Variables Page. The codebook for these variables, generated by FERRET, is given below:
AGER1 (AGE RECODE #1)
3 18-24 years
4 25-44 years
5 45-64 years
6 65-69 years
7 70-74 years
8 75 years and over
ADDSALT (HOW OFTEN ADD SALT TO FOOD)
1 Always
2 Often
3 Sometimes
4 Rarely
5 Never
8 Not ascertained
9 DK or refused
REGION (REGION)
1 Northeast
2 Midwest
3 South
4 West
SEX (SEX)
1 Male
2 Female
41 From the Select Variable Values Page, the 18-24 year age group, non-missing values for the ADDSALT variable, the Northeast and South regions, and all values for the SEX variable were selected. Selecting a cross-tabulation with ADDSALT as the column variable, REGION as the row variable, SEX as the page variable, and using the final basic statistical weight, produced the results in Table 3. Note that the use of statistical weights is the default option when creating a cross-tabulation. Students can then begin to address the research question using the information generated by FERRET.
Table 3. Weighted Counts and Percentages for Individuals Age 18-24 from the 1993 NHIS
| ADDSALT (how often add salt to food) | ||||||||
| SEX | REGION | Always | Often | Sometimes | Rarely | Never | Total | |
| Male | Northeast | Freq | 353,445 | 146,652 | 420,166 | 381,723 | 672,236 | 1,974,222 |
| Row % | 17.90 | 7.43 | 21.28 | 19.34 | 34.05 | |||
| South | Freq | 662,789 | 359,582 | 900,512 | 666,123 | 1,060,462 | 3,649,468 | |
| Row % | 18.16 | 9.85 | 24.68 | 18.25 | 29.06 | |||
| Total | Freq | 1,016,234 | 506,234 | 1,320,678 | 1,047,846 | 1,732,698 | 5,623,690 | |
| Female | Northeast | Freq | 252,933 | 224,059 | 452,305 | 492,934 | 706,602 | 2,128,833 |
| Row % | 11.88 | 10.52 | 21.25 | 23.16 | 33.19 | |||
| South | Freq | 828,953 | 506,387 | 917,390 | 691,746 | 824,580 | 3,769,056 | |
| Row % | 21.99 | 13.44 | 24.34 | 18.35 | 21.88 | |||
| Total | Freq | 1,081,886 | 730,446 | 1,369,695 | 1,184,680 | 1,531,182 | 5,897,889 | |
Source: FERRET, http://ferret.bls.census.gov/cgi-bin/ferret
42 As a second example, the following question will be considered. Are there regional differences in the amount of medical utilization for young adults? To address this question, the variable DV12, the number of doctor visits in the past twelve months, will be used. Since this variable is ordinal and has a large number of possible values, it is not well suited for description in a cross-tabulation. Therefore, the data will be downloaded using FERRET and analyzed using a separate statistical package. Depending on the other variables to be used, either the "Person File" or the "Year 2000" supplement could be used. In this example, the "Person File" was selected from the Survey Form Page. On the Data Search Page the following terms were entered: region, age, doctor visits, and wtfa (WTFA is the final statistical weight on the "Person File"). The variables AGER1, REGION, DV12, and WTFA were then selected. The codebook for the variable DV12 is listed below. As an example, a value of 3 indicates that there were three visits in the past year.
DV12 (DOCTOR VISITS IN PAST 12 MONTHS)
000 None
001-996 Visits
997 997+ Visits
998 Unknown
43 The 18-24 year age group, all values for REGION and values of DV12 between 0 and 997 were selected from the Select Variable Values Page. The "Create Ascii file for downloading" option was then selected. These data were then imported into a statistical package (such as SPSS, SAS, or STATA). The results in Table 4 were generated using the weight variable WTFA.
Table 4. Descriptive Statistics for Number of Doctor Visits in the Past 12 Months (DV12) by Region for Individuals Age 18-24 from the 1993 NHIS
| REGION | ||||
| Quantile | Northeast | Midwest | South | West |
| 100% | 360 | 248 | 160 | 156 |
| 99% | 25 | 30 | 30 | 32 |
| 95% | 13 | 12 | 12 | 13 |
| 90% | 8 | 8 | 7 | 8 |
| 75% | 3 | 3 | 3 | 3 |
| 50% | 1 | 1 | 1 | 1 |
| 25% | 0 | 0 | 0 | 0 |
| % with DV12 > 0 | 74.2 | 73.0 | 68.2 | 66.9 |
| Mean | 3.41 | 3.35 | 2.91 | 3.36 |
| Jackknife Standard Error |
0.46 | 0.21 | 0.12 | 0.22 |
Data Source: FERRET, http://ferret.bls.census.gov/cgi-bin/ferret
44 Students can begin to address the research question by considering the quantiles, percentages, and means in Table 4. A more advanced class could consider the treatment of outliers such as the maximum value in the Northeast of 360 doctor visits. This might bring up topics such as the use of a trimmed mean. Further investigation could include stratifying the analysis by various demographic variables such as sex, income, and smoking status.
45 Students in an independent study or an advanced class could generate confidence intervals using software such as SUDAAN or by constructing jackknife estimates of the standard error. The standard errors in Table 4 were generated in SAS using the variables CSTRATUM and CPSU as described in "Method 1 - Single Stage PSUs Sampled With Replacement within Strata Design for 1987-1994 NHIS" of the NCHS documentation for variance estimation in the NHIS ( http://www.cdc.gov/nchs/about/major/nhis/sudaan.htm).
46 There is a wealth of information contained in the data collected by the NHIS. There are countless investigations that can be performed using these data. To facilitate the use of the NHIS for class projects, some of the variables that are available on the "Person file" and the "Year 2000" supplement of the NHIS are listed in Table 5.
Table 5. Selected Variables from the 1993 NHIS
| File/Supplement | |||
| Variable Name | Person | Year 2000 | Description |
| SEX | X | X | sex |
| AGE | X | X | age |
| BIRTHMO | X | X | month of birth |
| PHONE | X | X | household has telephone |
| RACE | X | X | main racial background |
| MARSTAT | X | X | marital status |
| EDUC | X | X | education of individual -- completed years |
| INCFAM | X | X | family income |
| FAMSIZER | X | X | size of family |
| HEALTH | X | X | self reported current health status |
| EMPLOY | X | X | employment status in past 2 weeks |
| WKCLASS | X | X | class of worker (private, government, self-employed) |
| OCCUP | X | X | occupation detail code |
| HEIGHT | X | X | height without shoes |
| WEIGHT | X | X | weight without shoes |
| BDDAY12 | X | X | bed days in past 12 months |
| DV12 | X | X | doctor visits in past 12 months |
| HDA12X | X | X | non-delivery hospital days in past 12 months |
| REGION | X | X | region (Northeast, Midwest, South, West) |
| WTFA | X | X* | final annual statistical weight (w) |
| ANYSMOKE | X | anyone smoke inside the home | |
| SMOKDTEC | X | number of smoke detectors in home | |
| BUILT50 | X | was home built before 1950 | |
| SMKSTAT | X | current smoking status | |
| CIGPDAY | X | cigarettes now smoked per day | |
| CHEWTBC | X | chewing tobacco use | |
| WANTSTCG | X | want to completely stop smoking cigarettes | |
| ADDSALT | X | how often add salt to food | |
| RDINGR | X | how often read ingredient list on food | |
| RDCAL | X | how often read calorie, fat content on label | |
| WKHRS2 | X | usual hours worked per week | |
| HAVEASTH | X | ever told you have asthma | |
| SEATBLTF | X | wear seat belt in front seat | |
| SEATBLTB | X | wear seat belt in back seat | |
| FLUSHOT | X | had flu shot in past 12 months | |
| STRESSYR | X | amount of stress experienced in the past year | |
| STRSEFFT | X | effect of stress on health in past year | |
| ONWDIET | X | now trying to lose/gain weight | |
| BMASSIND | X | body mass index | |
| DESWGT | X | % above/below desirable weight (according to 1983 Metropolitan Life standards) |
|
* The variable name is FINBASWT on the Year 2000 supplement.
47 The use of a tangible example, such as the NHIS, can make the concepts of statistical sampling and topics in survey design more meaningful for college students. These concepts are especially relevant given the recent legal and political issues related to sampling.
American Statistical Association (1998), "Brief of Amicus Curiae," Alexandria, VA, https://www.amstat.org/outreach/amicus.html
Benson, V., and Marano, M. A. (1994), "Current Estimates from the National Health Interview Survey, 1993," National Center for Health Statistics, Vital and Health Statistics, Series 10, No. 110.
Ferber, R., Sheatsley, P., Turner, A., and Waksberg, J. (1980), "What is a Survey?," Subcommittee of the Section on Survey Research Methods, American Statistical Association.
Massey, J. T., Moore, T. F., Parsons, V. L., and Tadros, W. (1989), "Design and Estimation for the National Health Interview Survey, 1985-94," National Center for Health Statistics, Vital and Health Statistics, Series 2, No. 110.
Moore, D. S. (1998), "Statistics, Policy and ASA," Amstat News, Issue 256, p. 5.
Mulry, M., and Griffiths, R. (1996), "Comparison of CensusPlus and Dual System Estimates," 1995 Test Census Results Memorandum No. 43.
National Health Interview Survey (1993), NCHS CD-ROM Series 10, No. 7, Hyattsville, MD: National Center for Health Statistics.
Overton, W. S., and Stehman, S. V. (1995), "The Horvitz-Thompson Theorem as a Unifying Perspective for Probability Sampling: With Examples from Natural Resource Sampling," The American Statistician, 49, 261-268.
U.S. Census Bureau (1997), "Report to Congress -- The Plan for Census 2000," August Report, http://www.census.gov/main/www/2kplans.html
U.S. Census Bureau (1999), "United States Census 2000, Updated Summary: Census 2000 Operational Plan," February Report, http://www.census.gov/dmd/www/pdf/2000plan.pdf
Shah, B. V., Barnwell, B. G., and Bieler, G. S. (1997), SUDAAN User's Manual, Release 7.5, Research Triangle Park, NC: Research Triangle Institute.
Richard M. Single
Department of Mathematics
St. Michael's College
Winooski Park
Colchester, VT 05439
JSE Homepage | Subscription Information | Current Issue | JSE Archive (1993-1998) | Data Archive | Index | Search JSE | JSE Information Service | Editorial Board | Information for Authors | Contact JSE | ASA Publications