Ruma Falk
The Hebrew University of Jerusalem
Arnold D. Well
University of Massachusetts, Amherst
Journal of Statistics Education v.5, n.3 (1997)
Copyright (c) 1997 by Ruma Falk and Arnold D. Well, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the authors and advance notification of the editor.
Key Words: Association in 2 x 2 table; Correlation as probability; Inbreeding; Regression slopes.
Some selected interpretations of Pearson's correlation coefficient are considered. Correlation may be interpreted as a measure of closeness to identity of the standardized variables. This interpretation has a psychological appeal in showing that perfect covariation means identity up to positive linearity. It is well known that |r| is the geometric mean of the two slopes of the regression lines. In the 2 x 2 case, each slope reduces to the difference between two conditional probabilities so that |r| equals the geometric mean of these two differences. For bivariate distributions with equal marginals, that satisfy some additional conditions, a nonnegative r conveys the probability that the paired values of the two variables are identical by descent. This interpretation is inspired by the rationale of the genetic coefficient of inbreeding.
1 Pearson's product-moment correlation coefficient, r, is
ubiquitously used in education, psychology, and all the
social sciences, and the topic of correlation is central to
many statistical methods. Correlation is an important
chapter in introduction-to-statistics textbooks and courses
of all levels. Yet the diversified nature and subtle
nuances of this concept are not generally known. Some
confusion about r's interpretation is occasionally found in
the literature. As an extreme example, the common
interpretation of r² as the "proportion of variance in
Y explained or accounted for by X" has led to the claim
being made in a number of psychology textbooks that children
achieve about 50% of their adult intelligence by age 4. The
origin of this misleading statement can be traced to a
longitudinal study that found IQ scores at age 17 to have a
correlation of .71 with IQ at age 4 (see, e.g.,
Bloom 1964,
p. 57 and p. 68). The resulting r² of .50 (or 50%) does
provide some indication of how predictable adult IQ is from
IQ at age 4. Specifically, it indicates that if a linear
regression equation is used to predict adult IQ values from
IQ values at age 4, the ratio of the variance of the
predicted adult IQ scores (![]() )
to the variance of the
actual adult IQ scores (Y) should be .50, that is,
)
to the variance of the
actual adult IQ scores (Y) should be .50, that is,
However, this ratio says nothing about the relative levels of intelligence at age 4 and 17 (as pointed out by Myers and Well 1991, p. 395).
2 Our focus in this paper, is, however, not on the misuse or misconceptions of the correlation coefficient, but rather on the prolific nature of this measure. Limiting our teaching to the definition of r as "a measure of linear association" (and/or as a measure of fit to the regression line) may leave the conception of correlation rather impoverished. The more one deals with this coefficient, the more one discovers new meanings and different ways of looking at it. Teachers of statistics, who are aware of this wealth of possibilities, may enrich their teaching by offering new interpretations adapted for the problems discussed at different levels.
3 The diverse insights about what is conveyed by the correlation coefficient must be cautiously introduced, because the appropriateness of some interpretations is subject to specific constraints. One should carefully check, in each case, whether a given interpretation applies to the data at hand. In particular, teachers should realize that some interpretations of r are valid only under certain special conditions.
4 Several dimensions have to be considered when determining the applicability of an interpretation: First, does it hold for all possible values of r, or only for nonnegative values? Second, are any two marginal distributions allowed, or does the interpretation depend on having identical marginal distributions? Third, do we refer to any n x n distribution or only to 2 x 2 distributions?
5 In this article, we present some selected interpretations of the correlation coefficient classified by their content, or meaning, and we specify in each case the technical constraints imposed by the above three dichotomies. The case of 2 x 2 distributions with identical margins is the richest in turning out diverse and interesting interpretations of r. It is, however, often tempting to extend some appealing interpretations to situations beyond their legitimate domain. We illustrate one such case in detail.
6 Without pretense to covering all the meanings of correlation, we focus on arithmetic and conceptual interpretations, and on discrete variables, in a descriptive (and didactic) approach. (See Note 1.) In the second part of the Introduction, we mention several of the most common forms in which correlation is used and presented in teaching. Then, we discuss three untutored notions of the correlation coefficient which are often formed spontaneously in students' minds. These are partly justified, but not completely accurate preconceptions. Students tend to think intuitively of correlation as 1) indicating how close to identity two variables are; 2) a measure of our benefit from predicting one variable by the other one; or 3) the probability, or proportion of equality between the variables. We will show that although all three interpretations have some core of truth, they have to be either modified or qualified (by the type of variables or by some constraints on the bivariate distribution) in order to apply to specific situations.
7 Pearson's linear correlation coefficient, rxy, between two variables X and Y is defined by the formula
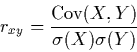 |
(1) |
All the other "faces of the correlation coefficient" described in this article may be derived from (1) and could be regarded as tautological. However, a rephrasing of a mathematical statement, although redundant on a formal level, may be psychologically and didactically instructive.
8 The correlation coefficient, as defined in (1), is described
by Rodgers and Nicewander (1988, p. 62)
as "standardized covariance" since it is equal to
Cov(zx, zy),
where zx
and zy denote the respective
standardized X and Y
variables. Furthermore, the computation of rxy
reduces to obtaining the arithmetic mean of the products of
zx and zy,
that is,
![]() (see, e.g., Cohen and Cohen 1975,
p. 34; Rodgers and Nicewander 1988;
Welkowitz, Ewen, and Cohen 1976, p. 159).
(see, e.g., Cohen and Cohen 1975,
p. 34; Rodgers and Nicewander 1988;
Welkowitz, Ewen, and Cohen 1976, p. 159).
9 A nonnegative r can be construed as the proportion of the
maximum possible covariance that is actually
obtained (Ozer 1985). This maximal value is
![]() .
When the variances of X and Y
are equal, (1) reduces to Cov(X,Y)/Variance, and a nonnegative
r equals the proportion of the variance that is attained by
the covariance.
.
When the variances of X and Y
are equal, (1) reduces to Cov(X,Y)/Variance, and a nonnegative
r equals the proportion of the variance that is attained by
the covariance.
10 When X and Y are dichotomous variables, their joint probability distribution can be arranged in a 2 x 2 table, as presented in Table 1. Let all the probabilities in this table be positive.
| X | |||
|---|---|---|---|
| Y | 0 | 1 | Total |
| 1 | p01 | p11 | p. 1 |
| 0 | p00 | p10 | p. 0 |
| Total | p0. | p1. | 1 |
11 Without loss of generality, we may assume that X and Y take on the values of 0 and 1. It can easily be shown that rxy in this case (also known as the phi coefficient) is given by
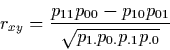 |
(2) |
(Cohen and Cohen 1975, p. 37; Hays and Winkler 1971, pp. 802-804). Formula (2) indicates that zero correlation occurs, in the 2 x 2 case, if and only if there is proportionality between the rows (columns) of the probability distribution. Dichotomous variables are thus noncorrelated whenever they are statistically independent.
12 The following sections deal with three different approaches to the interpretation of r: 1) r as an index of closeness to identity of standardized scores; 2) r as the (geometric) average of the regression slopes; 3) r as probability of common descent.
13 Perfect positive correlation does not mean identity of the paired values of the two variables, although sometimes beginners tend to think so. But it does mean identity up to positive linearity, that is, identity between the paired standardized values (Cahan 1987). There exists, accordingly, a formula for r, which is equivalent to (1), and which can be read as conveying the extent of closeness to identity of zx and zy:
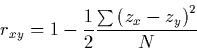 |
(3) |
where N is the number of paired observations. The derivation of (3) is elementary and is given in many sources (see, e.g., Cahan 1987; Myers and Well 1991, pp. 382-384; Rodgers and Nicewander 1988). The rationale of this approach to interpreting correlation is fully described by Cohen and Cohen (1975, pp. 32-34) and by Welkowitz, Ewen, and Cohen (1976, pp. 152-158).
14 There is undoubtedly a psychological appeal to regarding r
as a measure of closeness to identity (while keeping in mind
that one refers to standardized variables). The component
measuring departure from identity in (3) -- the mean of the
squared deviations -- is equal to
![]() (zx
- zy), or
to
(zx
- zy), or
to ![]() (dz),
where dz denotes the difference
zx - zy.
A simpler form of the formula is thus
r = 1 -
.5
(dz),
where dz denotes the difference
zx - zy.
A simpler form of the formula is thus
r = 1 -
.5![]() (dz).
It is now easy
to see what happens in some specific cases. When
zx = zy,
for example,
(dz).
It is now easy
to see what happens in some specific cases. When
zx = zy,
for example,
![]() (dz)
vanishes, and r = 1. When the covariance of
zx and
zy is zero,
(dz)
vanishes, and r = 1. When the covariance of
zx and
zy is zero,
![]() (dz) =
(dz) =
![]() (zx) +
(zx) +
![]() (zy) = 2,
and r = 0;
whereas, in the case of maximal departure from identity, that is,
when zx
= -zy,
(zy) = 2,
and r = 0;
whereas, in the case of maximal departure from identity, that is,
when zx
= -zy,
![]() (dz) = 4,
and r = -1.
(dz) = 4,
and r = -1.
15 Cahan (1987) highlights a didactic advantage of the closeness-to-identity interpretation. The correlation coefficient is interpreted as a measure of goodness of fit (of the standardized variables) to the identity line rather than to the least-squares prediction line. Thus, students' ability to comprehend what r means does not have to depend on their understanding the concept of regression, which is far from elementary. In addition, Cahan points out a shortcoming of the common interpretation of correlation as a measure of success of the linear-regression prediction: The goodness of fit to the regression line does not diminish monotonically when r decreases from 1 to -1, rather it varies monotonically with |r| and r2. Closeness-to-identity (of the z scores), in contrast, decreases with r over the whole range from 1 to -1. The case of r = -1 sharpens the disparity between the two interpretations: A correlation coefficient of -1 indicates the greatest possible departure from identity (of the zs) and at the same time maximal fit to the least-squares regression line. (See Note 2.)
16 Whenever a bivariate probability distribution has equal marginal distributions, cases of nonidentity between paired observations are considered misclassifications, namely, assignment of an item (pair) into different X and Y categories. Let P(m) denote the (total) probability of misclassification. It is obtained by summing all the probabilities of paired X and Y values that are unequal. The smaller the value of P(m), the greater the closeness to identity of the two variables (cf. Levy 1967; Ozer 1985).
17 In 2 x 2 distributions with identical marginals, where p and q denote the respective probabilities of 1 and 0, it is easy to verify that the equality of the marginal distributions entails equal probabilities in the two cells representing misclassifications, that is p01 = p10 (see Table 1). The bivariate distribution is thus symmetric about the secondary diagonal (i.e., the diagonal from the lower left corner to the upper right corner). In this case, r reduces to
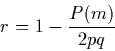 |
(4) |
When P(m) is zero, only the secondary diagonal of the 2 x 2
distribution contains nonzero probabilities
(p11 = p and
p00 = q), and r = 1.
When X and Y are classified
independently, this means that p01 =
p10 = pq, and
P(m) = 2pq, therefore r = 0. Formula (4) thus
presents r as the complement of the ratio of the actual P(m)
to the rate of misclassifications expected under independence.
If misclassifications are more probable than they are under
independence, r is negative. Maximal departure from
identity occurs when
18 The correlation rxy between X and Y is always bounded between the regression coefficient of Y on X, denoted byx, and that of X on Y, denoted bxy. These three numbers are all of the same sign, and they are connected by the formula rxy2 = byxbxy. Taking the square root of both sides of the formula, we see that a nonnegative r can be interpreted as the geometric mean of the two slopes of the regression lines (Rodgers and Nicewander 1988),
| |
(5) |
19 If the standard deviations of X and of Y are equal, the two
regression coefficients and the correlation coefficient are
all equal (in value and sign). In particular, r equals the
slope of the standardized regression lines:
![]() and
and
![]() (Cohen and Cohen 1975, p. 40,
Rodgers and Nicewander 1988). These two
equations mean that |r| conveys the extent to which one
should not "regress to the mean" when predicting by the
regression lines, thus confirming students' intuitive
conception of correlation as a measure of the efficacy of
our prediction.
(Cohen and Cohen 1975, p. 40,
Rodgers and Nicewander 1988). These two
equations mean that |r| conveys the extent to which one
should not "regress to the mean" when predicting by the
regression lines, thus confirming students' intuitive
conception of correlation as a measure of the efficacy of
our prediction.
20 In the 2 x 2 case, the slope of each regression line reduces
to the difference between two conditional probabilities. To
show this, we apply the formula byx =
Cov(X,Y) /![]() (X),
and use the notations of Table 1 to obtain
(X),
and use the notations of Table 1 to obtain
Replacing p.1 by p01 + p11 and using a little algebra,
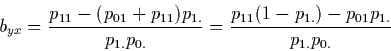
the regression coefficient of Y on X is transformed into
the difference between two conditional probabilities in the
horizontal direction (see Table 1).
Let ![]() denote this difference. We thus have,
denote this difference. We thus have,
Similarly, one gets in the vertical direction,
It can easily be verified that
![]() and
and
![]() stay unchanged when swapping roles between 0 and 1 in the above
formulas.
stay unchanged when swapping roles between 0 and 1 in the above
formulas.
21 Some authors have confused the difference between the two
conditional probabilities (in one of these directions) with
the correlation of the bivariate distribution: In studies
of intuitive judgment of contingency between two dichotomous
variables, the concept of correlation is often described as
"a comparison between two conditional probabilities"
(Shweder 1977, p. 638). Ward
and Jenkins (1965) maintain
that "perhaps the simplest formulation of contingency which
is adequate to the case of unequal marginal frequencies
involves a comparison of two conditional probabilities"
(p. 232). In a similar vein, Jennings, Amabile,
and Ross (1982) explain: "One satisfactory method, for example,
might involve comparing proportions (i.e., comparing the
proportion of diseased people manifesting the particular
symptom with the proportion of nondiseased people
manifesting that symptom)" (p. 213). The difference
between two conditional probabilities provides, however, an
answer to a directional question about the increase in the
conditional probability of a given value of one variable
given a one-unit change in the other variable. This
difference does not answer the two-way (symmetric) question
about the strength of association between the two variables.
The latter question is answered by the correlation
coefficient. Since
![]() =
byx and
=
byx and
![]() =
bxy,
it follows from (5) that a nonnegative r
of any 2 x 2 contingency table is the geometric mean of the
differences between the conditional probabilities in the two
directions, that is,
=
bxy,
it follows from (5) that a nonnegative r
of any 2 x 2 contingency table is the geometric mean of the
differences between the conditional probabilities in the two
directions, that is,
| |
(6) |
22 It should be kept in mind that two types of problems may be
formulated concerning the same 2 x 2 contingency table
(Allan 1980). A one-way problem asks about the
dependency of one variable on the other. The question, in this case,
is sometimes phrased in causal terms, as, for example, when
asking about the degree of control exerted by the seeding of
clouds over the occurrence of rain (Ward and Jenkins
1965). This type of question should be answered by
![]() of the
appropriate direction. A two-way problem asks about the
overall dependency between two variables in a nondirectional
way, as, for instance, when testing the stereotypical notion
that red-haired people are hot tempered. This question
should be answered by a symmetric measure of the extent to
which red hair is positively correlated with hot temper
(Jennings et al. 1982). Formula (6) for
r is appropriate here.
of the
appropriate direction. A two-way problem asks about the
overall dependency between two variables in a nondirectional
way, as, for instance, when testing the stereotypical notion
that red-haired people are hot tempered. This question
should be answered by a symmetric measure of the extent to
which red hair is positively correlated with hot temper
(Jennings et al. 1982). Formula (6) for
r is appropriate here.
23 If the 2 x 2 bivariate distribution has equal marginal
distributions, then
![]() =
=
![]() .
We may denote
this (common) difference between conditional probabilities
by
.
We may denote
this (common) difference between conditional probabilities
by ![]() . It follows from (6)
that
. It follows from (6)
that ![]() =
rxy.
Moreover, this equality holds for negative values of r as
well. Suppose the two categories of the independent
variable X represent control (X = 0) and treatment
(X = 1), and those of Y describe the treatment outcomes:
dead (Y = 0) and alive (Y = 1). Then
=
rxy.
Moreover, this equality holds for negative values of r as
well. Suppose the two categories of the independent
variable X represent control (X = 0) and treatment
(X = 1), and those of Y describe the treatment outcomes:
dead (Y = 0) and alive (Y = 1). Then
![]() shows the change
in survival rate associated with receiving treatment.
Consequently, in 2 x 2 contingency tables with equal
marginals, where r =
shows the change
in survival rate associated with receiving treatment.
Consequently, in 2 x 2 contingency tables with equal
marginals, where r =
![]() ,
the correlation coefficient
can be interpreted as the effect of treatment on the success
rate (Rosenthal and Rubin 1982). This
accords with construing r as a measure of our benefit, not
only from prediction, but from treatment as well.
,
the correlation coefficient
can be interpreted as the effect of treatment on the success
rate (Rosenthal and Rubin 1982). This
accords with construing r as a measure of our benefit, not
only from prediction, but from treatment as well.
24 In the specific case of a 2 x 2 frequency distribution, as
in Table 2, in which all four marginal totals are 100, the
difference between the number alive who received treatment
and the number alive in the control condition coincides with
![]() and r (when the
latter measures are expressed as
percentages). One can clearly "see" r when displayed in
such 2 x 2 contingency tables. Rosenthal and
Rubin (1982) advocate displaying effect sizes by means of such a
presentation, which they label binomial effect size
display (BESD); see also Rosenthal (1990)
and Rosnow and Rosenthal (1989).
and r (when the
latter measures are expressed as
percentages). One can clearly "see" r when displayed in
such 2 x 2 contingency tables. Rosenthal and
Rubin (1982) advocate displaying effect sizes by means of such a
presentation, which they label binomial effect size
display (BESD); see also Rosenthal (1990)
and Rosnow and Rosenthal (1989).
Table 2. Binomial Effect Size Display: A 2 x 2 Frequency Distribution with rxy = .32 (Based on Rosenthal and Rubin 1982, Table 1)
| Y (treatment outcome) |
X (condition) | ||
|---|---|---|---|
| 0 (control) | 1 (treatment) | Total | |
| 1 (alive) | 34 | 66 | 100 |
| 0 (dead) | 66 | 34 | 100 |
| Total | 100 | 100 | 200 |
25 Rosenthal and Rubin's (1982) interpretation
of r as the effect displayed by BESD is intuitively appealing.
It is, however, too limited by depending on distributions of the
type displayed in Table 2 with treatment and control groups
of equal size which is required to be 100. If we merely
impose the constraint that the 2 x 2 distribution has equal
marginal distributions, then r, in the range from -1 to 1,
may be interpreted as a modified BESD, or
![]() , that
is, the improvement rate attributable to moving from
"control" to "treatment."
, that
is, the improvement rate attributable to moving from
"control" to "treatment."
26 However, limiting the interpretation of r as
![]() to the
case of equal marginal distributions is essential.
Rosenthal (1990) and
Rosnow and Rosenthal (1989) have
apparently overstretched this interpretation by applying it
to the case of unequal marginal distributions. Table 3 uses
the data of Rosnow and Rosenthal's (1989)
Table 2, with frequencies converted to probabilities and the headings
changed to suit the previous survival-rate example.
to the
case of equal marginal distributions is essential.
Rosenthal (1990) and
Rosnow and Rosenthal (1989) have
apparently overstretched this interpretation by applying it
to the case of unequal marginal distributions. Table 3 uses
the data of Rosnow and Rosenthal's (1989)
Table 2, with frequencies converted to probabilities and the headings
changed to suit the previous survival-rate example.
Table 3.
Bivariate Probability Distributions with Correlation Coefficient .034 (Based on the Data in Table 2 of Rosnow and Rosenthal 1989)
| Y (treatment outcome) |
X (condition) | ||
|---|---|---|---|
| 0 (control) | 1 (treatment) | Total | |
| (a) Original data | |||
| 1 (alive) | .4913 | .4954 | .9867 |
| 0 (dead) | .0086 | .0047 | .0133 |
| Total | .4999 | .5001 | 1.0000 |
| (b) BESD | |||
| 1 (alive) | .2415 | .2585 | .5000 |
| 0 (dead) | .2585 | .2415 | .5000 |
| Total | .5000 | .5000 | 1.0000 |
27 Part (a) of the table presents the original 2 x 2 distribution with unequal marginal distributions and r = .034, and part (b) presents a binomial effect size display (BESD) of the same r via a 2 x 2 distribution with equal and uniform marginal distributions.
28 Note that although in both parts rxy = .034, one can interpret this coefficient as the change in survival probability associated with receiving treatment only in the BESD case. Indeed, in part (b), we obtain
In the original distribution (part (a)), however, although r = .034, "the change in survival probability associated with receiving treatment" is
Thus the improvement in survival rate affected by treatment differs from r for this distribution. The fact that in another 2 x 2 distribution with the same r the "improvement in survival rate" equals r does not mean that this interpretation applies to the correlation coefficient of the original data.
29 To sum up, in the 2 x 2 case, the question about the change
in success rate attributable to treatment is directional.
It should be answered by
![]() .
When the marginal distributions are the same,
.
When the marginal distributions are the same,
![]() =
=
![]() =
=
![]() =
rxy, and the question is answered by
rxy as
well. Generally, however, we see from formula (6) that
=
rxy, and the question is answered by
rxy as
well. Generally, however, we see from formula (6) that
![]() may differ from rxy (if
may differ from rxy (if
![]() ),
as in part (a) of Table 3. The
),
as in part (a) of Table 3. The
![]() interpretation of r
should therefore be cautiously applied.
interpretation of r
should therefore be cautiously applied.
30 Since r is a measure whose absolute value is bounded between 0 and 1, some students tend to erroneously interpret it as the proportion of identical x,y pairs or the probability of correct prediction (Eisenbach and Falk 1984). The teaching of correlation as a measure of linear association discourages such interpretations. (See Note 3.) Surprisingly, it turns out that in the case of dichotomous variables with equal marginals, a nonnegative r conveys the probability that the paired values are identical due to a common source. This interpretation was originally developed in the context of population genetics. It can, however, be extended with caution to other areas as well (Falk and Well 1996).
31 The phenomenon of inbreeding is said to occur when offspring are produced by parents who are more closely related than randomly selected members of the population. Without inbreeding, the offspring may be homozygous for a gene because of chance pairing of the same alleles. In the case of inbreeding, both parents may carry the same allele obtained from a common ancestor. Hence the probability that their offspring are homozygous for a given gene is greater than expected by independent pairing.
32 Two apparently different suggestions about how to quantify the degree of inbreeding of an individual happen to coincide. One suggestion defines the inbreeding coefficient, I, as the probability that the two paired alleles for a given gene are identical by descent. The other measures inbreeding via the correlation between the values of the alleles contributed by the two parents (Crow and Kimura 1970, pp. 64-69; Roughgarden 1979, pp. 177-186). The fact that for nonnegative values of r the two measures are equal allows r to be interpreted as the probability of identity by descent.
33 If the two alleles of a given gene are assigned the values 1 and 0 and their respective probabilities in the population are p and q (where p + q = 1), then the joint probability distribution of the allele values received from each parent, when the probability of common descent is I, is given in Table 4.
Table 4.
Probabilities of All Possible Genotypes, with Two Alleles and Inbreeding Coefficient I
| Value of sperm: Y |
Value of egg: X | ||
|---|---|---|---|
| 0 | 1 | Total | |
| 1 | (1 - I)pq | Ip + (1 - I)p2 | p |
| 0 | Iq + (1 - I)q2 | (1 - I)pq | q |
| Total | q | p | 1 |
34 For example, there are two ways both alleles can have the value 1: either they are derived from the same allele of the same ancestor (with probability I) and have the value 1 (with probability p), or they are randomly combined (with probability 1 - I) and both have value 1 (probability p2).
35 The correlation coefficient, r, between X and Y of Table 4 can easily be shown to equal I, the probability of identity by descent (see Falk 1993, pp. 81-84, 211-215, and Falk and Well 1996). We see further in Table 4 that I = r also measures the fraction by which heterozygosity is reduced (Crow and Kimura 1970, p. 66), that is, 1 - I is the multiplicative factor by which heterozygosity is changed relative to the case of independence. This interpretation of I and r is valid for the range from -1 to +1, so that negative correlation and inbreeding coefficients signify an increase, instead of decrease, in heterozygosity.
36 Moreover, the four probabilities of any 2 x 2 probability distribution with identical marginal distributions are uniquely determined by p, q, and r. This means that, independent of context, any 2 x 2 probability distribution with equal marginals is structured as in Table 4, with r taking the place of I. Thus, r -- whether positive, zero, or negative -- conveys the fraction by which inequality is decreased, relative to independence. In addition, a nonnegative r of such a distribution may be interpreted as the probability of inherent (i.e., nonchance) equality between the variables.
37 In the context of interjudge agreement, when two judges (e.g., for admission to medical school) assess the same set of objects (applicants) and make dichotomous decisions (accept or reject) while conforming to the same identical marginal distributions (depending on the percentage of available places), r measures their probability of nonchance interrater agreement (see Zwick 1988). The nonchance agreement may result, for instance, from the judges consulting each other about a proportion r of the cases and making a joint decision (while matching the predetermined distribution). The rest of the objects, of proportion 1 - r, are assigned by chance to one of the two categories, independently by each judge (subject to the same distribution). In this case, r is the percentage of nonindependent decisions (Falk and Well 1996).
38 Although the interpretation of r as probability of common descent is limited to the case of two dichotomous variables with equal marginal distributions, 2 x 2 contingency tables of identical marginals are not that rare. The population-genetic framework is obviously the best example in which the "inbreeding interpretation" of r applies. However, equal marginals are frequently encountered in psychological research (e.g., in the procedure known as Q-technique which involves paired judgments, see Falk and Well 1996).
39 Binary sequences occur in various behavioral domains. In learning studies, the data often comprise a series of successes and failures in consecutive trials. The same is true for sequential performance data in psychophysical and ESP research. Sports records, like those of basketball, include series of hits and misses of many players; and subjects are instructed to simulate chance binary sequences in studies of generation of randomness. One way of summarizing the sequential dependency in a binary series is by computing its serial correlation coefficient (see, e.g., Gilovich, Vallone, and Tversky 1985; Kareev 1995) which is based on a table constructed of the fourfold success/failure combinations which occur on all consecutive (overlapping) pairs of steps. Such a 2 x 2 distribution necessarily has (either exactly or very nearly) equal marginal distributions which coincide with the distribution of 1s and 0s along the binary sequence.
40 A nonnegative serial correlation thus conveys the probability that two successive symbols are "inherently equal," or that they originate from a "common source/cause" (the meaning of these statements depending on the context). When r is negative, its absolute value (which can attain the maximum, 1, only in the case of equiprobable binary symbols) indicates the rate of increase in the tendency to alternate, relative to a sequence in which successive symbols are independent of each other. Regardless of sign, a serial-correlation coefficient can be interpreted as the proportion by which the alternation rate is reduced. This is true with respect to the conditional probabilities of change of symbol, following each of the two binary symbols.
41 The story of construing the meaning of Pearson's correlation develops in a strange way. First, we learn the formula for measuring the extent of linear association between two variables, only later do we discover other hidden meanings and realize that this remarkable coefficient answers many different questions. Whereas this course of learning is apparently natural for students, their teachers would better be familiar with r's diverse interpretations and their limitations so as to introduce them gradually when the proper circumstances come up.
42 We have shown that, in accordance with beginners' intuition, r can be interpreted as a direct index of the degree of closeness between two variables, provided one refers to standardized variables. We have dwelt in particular on the case of two dichotomous variables with equal marginal distributions. Several lay intuitions about the meaning of correlation turn out justified in this case: The coefficient measures the effectiveness of predicting one variable by the other. This is expressed by r as the difference between the two conditional probabilities involved in the prediction. When the categories of the predictor are "control" and "treatment," r conveys the effect of treatment on success rate (BESD).
43 The 2 x 2 case with equal marginals also permits interpretation of a nonnegative r as the probability of nonchance equality between the two variables. This nonchance match may be viewed in some cases as due to a common origin of the paired values. Interpreting r as a probability goes contrary to common caveats and requires some rethinking of the meaning of the concept of correlation.
This study was supported by the Sturman Center for Human Development, the Hebrew University, Jerusalem. We are grateful to Raphael Falk for his continuous help in all the stages of this study.
Note 1: Formulas tying r to various test statistics -- thus suggesting additional interpretations -- can be found, for example, in Cohen (1965), Friedman (1968), Levy (1967), Rodgers and Nicewander (1988), and Rosenthal and Rubin (1982). Geometric and trigonometric interpretations of r can be found, among other sources, in Cahan (1987), Guilford (1954, pp. 482-483), and Rodgers and Nicewander (1988).
Note 2: Note that the formula for Spearman's rank-order coefficient, rS, when there are no ties,
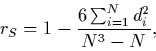
where di denotes the difference between the ranks of the ith pair, is structured similarly to (3). Spearman's rS is thus a measure of closeness to identity of the matched sets of ranks (see Cohen and Cohen 1975, p. 38, and Siegel and Castellan 1988, pp. 235-241).
Note 3: Recently, Rovine and von Eye (1997) showed that when k of the n standardized values of the variables X and Y are identical (i.e., there are k matches) and the other n - k values are unrelated, the (nonnegative) correlation coefficient between X and Y approximately equals the proportion of matches.
Allan, L. G. (1980), "A Note on Measurement of Contingency Between Two Binary Variables in Judgment Tasks," Bulletin of the Psychonomic Society, 15, 147-149.
Bloom, B. S. (1964), Stability and Change in Human Characteristics, New York: Wiley.
Cahan, S. (1987), "On the Interpretation of the Product Moment Correlation Coefficient as a Measure," unpublished manuscript, The Hebrew University, School of Education, Jerusalem, Israel.
Cohen, J. (1965), "Some Statistical Issues in Psychological Research," in Handbook of Clinical Psychology, ed. B. B. Wolman, New York: McGraw-Hill, pp. 95-121.
Cohen, J., and Cohen, P. (1975), Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, Hillsdale, NJ: Lawrence Erlbaum.
Crow, J. F., and Kimura, M. (1970), An Introduction to Population Genetics Theory, New York: Harper & Row.
Eisenbach, R., and Falk, R. (1984), "Association Between Two Variables Measured as Proportion of Loss-Reduction," Teaching Statistics, 6, 47-52.
Falk, R. (1993), Understanding Probability and Statistics: A Book of Problems, Wellesley, MA: AK Peters.
Falk, R., and Well, A. D. (1996), "Correlation as Probability of Common Descent," Multivariate Behavioral Research, 31, 219-238.
Friedman, H. (1968), "Magnitude of Experimental Effect and a Table for Its Rapid Estimation," Psychological Bulletin, 70, 245-251.
Gilovich, T., Vallone, R., and Tversky, A. (1985), "The Hot Hand in Basketball: On the Misperception of Random Sequences," Cognitive Psychology, 17, 295-314.
Guilford, J. P. (1954), Psychometric Methods (2nd ed.), New York: McGraw-Hill.
Hays, W. L., and Winkler, R. L. (1971), Statistics: Probability, Inference, and Decision, New York: Holt, Rinehart & Winston.
Jennings, D. L., Amabile, T. M., and Ross, L. (1982), "Informal Covariation Assessment: Data-Based versus Theory-Based Judgments," in Judgment Under Uncertainty: Heuristics and Biases, eds. D. Kahneman, P. Slovic, and A. Tversky, Cambridge: Cambridge University Press, pp. 211-230.
Kareev, Y. (1995), "Positive Bias in the Perception of Covariation," Psychological Review, 102, 490-502.
Levy, P. (1967), "Substantive Significance of Significant Differences Between Two Groups," Psychological Bulletin, 67, 37-40.
Myers, J. L., and Well, A. D. (1991), Research Design and Statistical Analysis, New York: HarperCollins.
Ozer, D. J. (1985), "Correlation and the Coefficient of Determination," Psychological Bulletin, 97, 307-315.
Rodgers, J. L., and Nicewander, W. A. (1988), "Thirteen Ways to Look at the Correlation Coefficient," The American Statistician, 42, 59-66.
Rosenthal, R. (1990), "How Are We Doing in Soft Psychology?" American Psychologist, 45, 775-777.
Rosenthal, R., and Rubin, D. B. (1982), "A Simple, General Purpose Display of Magnitude of Experimental Effect," Journal of Educational Psychology, 74, 166-169.
Rosnow, R. L., and Rosenthal, R. (1989), "Statistical Procedures and the Justification of Knowledge in Psychological Science," American Psychologist, 44, 1276-1284.
Roughgarden, J. (1979), Theory of Population Genetics and Evolutionary Ecology: An Introduction, New York: Macmillan.
Rovine, M. J., and von Eye, A. (1997), "A 14th Way to Look at a Correlation Coefficient: Correlation as the Proportion of Matches," The American Statistician, 51, 42-48.
Shweder, R. A. (1977), "Likeness and Likelihood in Everyday Thought: Magical Thinking in Judgments About Personality," Current Anthropology, 18, 637-658.
Siegel, S., and Castellan, N. J. (1988), Nonparametric Statistics for the Behavioral Sciences (2nd ed.), New York: McGraw-Hill.
Ward, W. C., and Jenkins, H. M. (1965), "The Display of Information and the Judgment of Contingency," Canadian Journal of Psychology, 19, 231-241.
Welkowitz, J., Ewen, R. B., and Cohen, J. (1976), Introductory Statistics for the Behavioral Sciences (2nd ed.), New York: Academic Press.
Zwick, R. (1988), "Another Look at Interrater Agreement," Psychological Bulletin, 103, 374-378.
Ruma Falk
Department of Psychology
The Hebrew University
Jerusalem, 91905 Israel
Arnold D. Well
Department of Psychology
Tobin Hall
University of Massachusetts
Amherst, MA 01003
A postscript version of this article (falk.ps) is available.