Lena Zetterqvist
Lund University
Journal of Statistics Education v.5, n.1 (1997)
Copyright (c) 1997 by Lena Zetterqvist, all rights reserved. This text may be freely shared among individuals, but it may not be republished in any medium without express written consent from the author and advance notification of the editor.
Key Words: Take-home projects; Small class versus large class situation.
By putting emphasis on applications in two basic statistics courses for chemistry students and chemical engineering students we have enhanced student motivation and increased student activity. In addition to a traditional in-class exam, the students complete a take-home project where statistical problems relevant to chemists are discussed. We give several examples of the course and project material. The main difference between the two courses is that the first is optional, attracting approximately 15 students, while the second is compulsory with approximately 100 students. We discuss how the different requirements affect the learning situation and how separate strategies of teaching have to be developed for the small class and large class situations, respectively.
1 Courses in statistics for scientists and engineers have often failed to raise interest or comprehension among the students, for several reasons:
2 Statistics educators during the last decade have discussed how to change statistics education for scientists and engineers by having more applied courses (Cobb 1993; Hogg 1985, 1991; Romero et al. 1995). Garfield (1995) gives a review of statistics education research and presents several principles of learning statistics. Some of these principles are cited below and their implications for statistics education are discussed.
3 In the project ``Statistics for chemistry students,'' the aim was to increase motivation and comprehension in a first statistics course for chemistry students by updating material and methods and focusing on the application of statistics.
4 Considering the principles presented by Garfield (1995) and stated above, the project for chemistry students, funded by the Swedish Council for the Renewal of Undergraduate Education, emphasizes teaching based on real chemical datasets and on problems relevant to chemists. An interactive statistical computer program is used to increase the possibilities of analysing real data in a ``nontrivial'' way. Final grades are determined by an in-class exam and a written, as well as an oral, account of a take-home project, using real data from the chemical world, where small groups of students solve a statistical problem on their own. The course was originally developed for a small-class situation but has been adapted to a large-class situation, and we report experiences from both kinds of courses and discuss differences between them.
5 Statistics courses for chemistry and chemical engineering students have been discussed in the literature. Eckert (1996) reports results of a survey that he sent to 172 chemical engineering departments in the United States and Canada in order to summarize the status of statistics-related education in chemical engineering. Two interesting projects, where statistical concepts are introduced and reinforced in undergraduate chemical engineering laboratories, are separately reported in Roberts, Johnson, and Gorton (1990) and in Nelson and Wallenius (1993). A similar approach is reported by Goedhart and Verdonk (1991), who also discuss how chemistry students in a laboratory course misinterpret certain statistical concepts, e.g., by thinking of error in a personal way as `` mistakes.'' Kopas and McAllister (1992) present different hands-on exercises developed for a short course in the chemical industry.
6 The small-class course for chemistry students was an entirely new statistics course when our project started. It is an optional course, attracting mainly second- or third-year students with at least two introductory courses in chemistry. The number of students varies between 10 and 15 each period.
7 The statistics course, which extends over 50 hours of lessons during eight weeks, is divided into modules of three lessons each. The modules are mixtures of traditional lectures (presenting new theory), of discussions and calculation (studying chemical examples and/or exercises given as homework), of laboratory work with the statistical package Statgraphics, and of guidance of the project work. To further motivate the students, a teacher from the Department of Chemistry has on some occasions acted as a guest lecturer, giving examples of statistical problems in chemical industries and research.
8 The examination consists of an in-class exam where basic statistical knowledge is tested and, at the end of the course (after the in-class exam), a project with both a written and an oral account. In the take-home projects, the students work in groups of two and choose between 8 and 10 different assignments. The oral account has a certain routine: two groups, with different assignments, present their work for each other (no teacher present). Afterwards, each group has to explain to the teacher the results of the fellow group. There are several advantages to this approach. Each student experiences at least two different assignments, he/she has extra training in verbal communication with statistical concepts, and the situation is a natural starting point for a discussion of the presented work. The take-home projects must be approved but are not graded, and the grade on the in-class exam becomes the final grade for the course.
9 Some of the take-home projects, which are continuously revised between different offerings of the course, have the ambition not only to illustrate and repeat already known statistical theory, but also to introduce the student to further statistical ideas.
10 Approximately six to eight hours is scheduled for laboratory work using the interactive statistical package Statgraphics, which is also used in the take-home projects. A small handbook on how to use the package is given to the students.
11 The material used consists of a basic course text and working material. The course text (Olbjer 1996) contains many examples with chemical applications and has recently been rewritten using experiences from the courses. Other material used in classroom sessions, e.g., problems discussed, examples and exercises, hand-outs for the interactive computer sessions, old exams and problems used as projects, is collected as material for guidance (Zetterqvist 1996) and is revised each time the course is given.
12 Suitable course material was found by
13 Besides the text material and examples developed for the course, the most positive effect of the project is the cooperation started with the Chemistry Department. Because the course for chemistry students was entirely new (and later a new course for chemical engineering students was developed), it was natural to make initial contacts. So far, three different teachers have actively been co-writing text material for the course, but the effect is spreading, and discussion is now turning more to the problem of introducing statistical elements in chemistry courses. One teacher, who has been working on a project funded by the Swedish Council for the Renewal of Undergraduate Education, has been very helpful in discussions and in establishing contacts with other teachers.
14 Below is given a description of the content of the course together with examples of chemical applications. Some of these examples are described in the next section. When data material are from statistical literature, references are given.
EXAMPLE 1: Copper in wood -- reanalysing a chemical laboratory experiment
15 In one of the first chemistry courses, the chemical engineering students determine the concentration of copper in a piece of impregnated wood. Each laboratory group makes a series of ten measurements (series 1) and after a short pause another series of three measurements (series 2). After the experiment, the students are told that the true value of the copper concentration is 100 ng/ml, and they conclude in this chemistry course that their measurements vary and may be systematically too low (or high).
16 In the statistics course, where data from all laboratory groups are presented, this dataset is used several times to illustrate different statistical concepts. Some examples are different kinds of errors (random error, systematic error, outliers), point and interval estimates of mean and standard deviation and how they depend on the number of measurements (by comparing series 1 and 2), and how a systematic error or differences between groups may be verified (one-sample and two-sample t-tests and ANOVA).
17 Incidentally, the students are always surprised at how ``clumsy'' they and their friends were as beginners in the laboratory.
EXAMPLE 2: The distribution of particle size
18 In a chemistry course preceding the statistics course, the chemical engineering students come across several situations where it is crucial to know how particle sizes are distributed. After repeating some of these situations, the students are given a dataset with particle sizes obtained by sieving. These data can be described by a lognormal distribution, and some typical characteristics of this distribution are given.
19 By using different types of sampling procedures, the
particle size can be measured by length, surface area, or
volume. By simulation the students find that if the
diameter (X) of the particle is lognormal, the surface area
and the volume (essentially ![]() and
and
![]() ) are
also lognormally distributed and that the estimated
parameters in the simulations are in agreement with the
theoretical values.
) are
also lognormally distributed and that the estimated
parameters in the simulations are in agreement with the
theoretical values.
20 Finally, they use simulations to illustrate how a mixture of two different types of particles (both lognormal) may, under certain values of the parameters, be recognized as a mixture while with other parameter values it is impossible to separate the two different types of particles. The problem with a mixture of distributions is motivated by two pharmaceutical examples.
21 This example was developed with and written in cooperation with a teacher of the Department of Chemistry who is the lecturer in the actual chemistry course. Distributions of particle size are discussed in Herdan (1960).
EXAMPLE 3: Determination of the distribution coefficient -- reanalysing a chemical laboratory experiment
22 In this laboratory experiment (compulsory for chemistry students), the students have to determine the distribution coefficient K_f of how iodine is distributed between heptane and water at 25 degrees C. In the laboratory guide, which is reproduced in the statistics course text, the formula for the coefficient is derived:
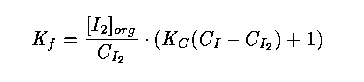
where
C_{I_2} is total concentration of iodine in the water, which is estimated by the average value of three titrations,
[I_2]_{org} is concentration of organic iodine, which is estimated by the average value of three titrations,
C_I is a known concentration of iodide in the water, and
K_C is a known value from a table.
In the statistics course the precision of the estimated value of K_f may be studied. The students explain the kinds of errors present and how they are propagated to the estimate of K_f. They are also asked to study how the variance of the estimate is affected if the number of titrations increases.
EXAMPLE 4: Spectrophotometric measurements of copper content in brass -- reanalysing a chemical laboratory experiment
23 In this laboratory experiment, which is compulsory for all chemistry students during their first term in the Department of Chemistry, the students come across the important problem of calibration. The absorbance of light in a solution with a given amount of copper concentration is measured with spectrophotometric equipment. Using the law of Lambert-Beer, the molar absorbance (A) can be expressed as a linear function of the concentration (c) of copper:
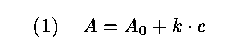
where A_0 and k are constants depending on the specific conditions of the experiment (e.g., wavelength of the light and temperature of the solution). In the experiment the students are told to measure molar absorbance for different solutions with known copper concentrations and to estimate the calibration function (1). Finally, they are asked to estimate an unknown concentration of copper in a solution by using the measurement of its absorbance and the estimated calibration function.
24 New insight into this problem, which for the students is based on well-known chemical theory, is provided in the statistical course. By introducing the statistical model of linear regression, the students can reanalyse their experiments, studying not only how the best estimates of the calibration function and the unknown copper concentration are made, but also what precision these estimates have. Further, the experiment is a natural starting point for discussion of how a calibration experiment should be designed or for a discussion of different kinds of errors in an experiment and how they propagate.
EXAMPLE 5: Central composite experimental designs applied to chemical systems -- introducing response surface techniques
25 In chemical systems one is often interested in how a variable is influenced by other variables or factors in the system. A response surface is a plot of the system response (e.g., percentage yield of a reaction) versus each of the factors or variables that have an influence on the response (e.g., temperature and pressure). One may wish to estimate the response surface or to find the optimum value of the response (or the values of the influencing factors that give the optimum response).
26 The students are presented with an experiment where the absorbance response from a constant volume of a solution of vanadyl sulphate (VOSO_4) is investigated as a function of the volume in drops of hydrogen peroxide (H_2O_2) and sulphuric acid (H_2SO_4). The chemical theories behind the reaction are explained and the experimental data given. With the knowledge of multiple linear regression and a good statistical package, the students start to estimate and plot response functions. They can interpret the parameters in the statistical model in chemical terms and discuss how an extended experiment should be designed.
27 This example is written in cooperation with a teacher in the Department of Chemistry and is based on an experiment described in Palasota and Deming (1992).
EXAMPLE 6: Nitrogen oxides in an area heated by natural gas furnaces -- statistical analysis of a large dataset
28 In this example the students are given a large dataset of measurements of nitrogen oxides made in a residential area with small houses where each home is heated by its own natural gas furnace. The village is situated in a suburban region between two cities and is surrounded by several highways with heavy traffic, as well as vast areas of farmland. During a period of five months the concentration of nitrogen oxides was continuously sampled by 25 different samplers. Variables such as wind direction, wind speed, and temperature were measured simultaneously. A description of the experiment and of the chemiluminiscent analyser used for the nitrogen oxides is given to the students.
29 The students are faced with several problems: How should data be described? How does the direction of the wind and wind speed affect the concentration of nitrogen oxides at a fixed sample point? Is there a significant contribution of nitrogen oxides from the gas furnace? There is a critical limit set by the Swedish National Environmental Protection Agency; how often is the limit exceeded?
30 When studying this dataset, the students are required to handle large datasets, perform data quality control, fit distributions to data, verify significant differences, and study relations between variables.
31 But, as in many real datasets, there are also problems not directly linked to the course content that are of great practical importance. The students discover that exceedances of the critical limit often occur in clusters. The students realize that they need to decluster the exceedances before attempting to fit an extreme value distribution.
32 The experiment is described in Vannerberg and Holmstedt (1989) and analysed in Lindgren, Zetterqvist, and Holmstedt (1993).
33 The responses from the students are documented in different ways. They consist of written evaluations performed immediately after the course, documented personal interviews after one of the courses (Zetterqvist 1994), and as a part of the result of a written student inquiry six months after the course for evaluation of the entire undergraduate statistics education at the department (Evaluation of Undergraduate Statistics Education in Mathematical Statistics 1995).
34 The student reactions to the course as a whole were positive. Nearly all students thought that their achieved knowledge would be useful in future studies and work, and many (about 65%) could contemplate attending a further statistics course. Most of them found the problems adequate and interesting. One student wrote: ``I found the course more interesting than I thought (had heard) it would be.'' The quote, which is a rather typical response, reflects the problem of students' (often negative) attitude to statistics before attending a course. This problem is discussed in Gal and Ginsburg (1994).
35 Most students appreciated the mixture of lectures, discussions, and exercises during the lessons because it allowed them to be more active. They found it positive to work with real chemical datasets and problems, and to use their achieved knowledge on the projects. ``I had to think for myself -- it was useful.'' The small-group activities including discussions with fellow students were also appreciated.
36 The communication between student and teacher increased, as well as between students themselves. We learned that it is important to be very clear in the outline of the projects, especially what is expected from the students. Great care should also be taken in the written guidance of the projects; instructions that are too detailed can make it boring, and those that are too vague can make it difficult. For future courses we plan to insert in the working material a student's report from a former take-home project as a good example.
37 Can a working applied statistics course for 15 students be transformed into a course for 100 students and still maintain its applied character? Is it practicable to use take-home projects and give personal guidance to such a large number of students? The small-class course is mainly optional with at least some well motivated students. Is it possible to increase student motivation in a large compulsory course and make it more enjoyable? These were the challenging questions when we started to develop a new course for chemical engineers based on the material developed for the small-class course. After giving the large-class course once, we think the answer is yes, but of course some modifications have to be made.
38 The large-class course has a rather interesting background. Ten years ago a small course was given by statisticians to chemical engineering students, but with no success. The Department of Chemistry decided to develop a statistics course of their own, but the result was a course on a statistical level that was too high for the students. After a few years the statisticians were back on scene again, but now with a course and a course literature that had been developed mainly for an industrial application. The course was still small; the elementary statistical concepts were covered but there was no time (or suitable examples) for chemical applications. Most of the students found the course ``easy'' (because the examination consisted of an in-class exam with standard problems), but boring and uninteresting. This was the situation when the Chemistry Department wanted to extend the course, and it was a golden opportunity for us to use experiences from the small-class course for chemistry students.
39 The number of students, scarcity of teachers, and central planning of the timetable forced us to organize the course in a more traditional schedule where lectures and exercises are separated. The large-class course consisted of 28 hours of lectures, 28 hours of exercises, and 14 hours of computer work in laboratory (6 hours of these were compulsory, the other 8 optional). Traditionally, the engineering students do most of their exercises at scheduled hours at school (with the assistance of a graduate student or an older student), and no homework is given as in the case of the chemistry students.
40 More hours were devoted to computer exercises than before, now using the program MATLAB because it is used in several courses in the syllabus for chemical engineering. We introduced more simulation, which is done excellently in MATLAB, and used its Statistics Toolbox of written routines in the parts of the course that consisted of more data analysis.
41 The separation of lectures and exercises decreased discussions during lectures drastically (it is easier to ask questions when 15 fellow students are listening than 100), but to some extent this was compensated for during the scheduled exercises. We tried to keep the applied character of the course by presenting the chemical examples on hand-outs for each lecture, and we tried to make them clearer than before. The computer exercises were also redeveloped to be more self-instructed.
42 We retained the take-home project as a part of the examination because we consider this a vital part of the course. However, some modifications had to be made. Instead of having students choose from among several take-home projects, we used one project with several possible statistical problems and a large set of data that we separated into submaterials for different student groups. We found that the design of the take-home project was even more crucial in this large-class situation, and that careful coordination between the teachers giving guidance was needed. The large number of students made it impossible to maintain the oral part of the examination. Instead, only a written report on the project and an in-class exam were required. As before, the grade on the in-class exam decides the final grade of the course, and the take-home project has to be passed.
43 The student reactions to the take-home project ranged from ``the highlight of the course'' to ``skip it,'' with a clear median of ``instructive.'' This group of students has traditionally not worked with statistical problems on their own and are accustomed to small standard problems where the answers can be quickly found in the course text.
44 Demanding more activity from the students also demands that teachers be more active. Initially, it means more work because their role as teachers is changed from the traditional lecturer to more guidance of the student in the take-home project.
45 Our overall experience from the large-class course is quite positive. Needless to say, the course material still has to be worked on, but the largest problem is quite different. For financial reasons it will probably be impossible to maintain the total number of hours spent on the course. One strategy is to reduce the number of hours for exercises and require the students to work more with them at home. Some of the students already use this way of learning.
46 The optional computer hours could be reduced or deleted, and the material could be made available on the computer network as self-instructed exercises. To make sure that the student is well prepared, the compulsory computer activities already include questions that the students must answer before they are allowed to start the computer exercise.
47 If scheduled hours spent on exercises and computer exercises have to be reduced, it will make the take-home project even more essential to the course. Skipping the project would take the course back to the stage of an uninteresting and boring course. We feel that the effect the take-home project has on the course as an assessment tool is considerable. However, the guidance of the project may have to be more ``centralized,'' perhaps concentrated in lectures.
48 Our conclusion is that even if the hours of the course have to be reduced, the applied character could be maintained. In fact, we feel that in this situation it has to be maintained. The fewer hours a teacher spends on an applied course, the greater need there is for important and interesting applications.
This project was supported by the Swedish Council for the Renewal of Undergraduate Education. We are grateful to the referees for their valuable comments and helpful suggestions, which considerably improved the paper.
Cobb, G. (1993), "Reconsidering Statistics Education: A National Science Foundation Conference," Journal of Statistics Education [Online], 1(1). (http://jse.amstat.org/v1n1/cobb.html)
Draper, N., and H. Smith (1981), Applied Regression Analysis (2nd ed.), New York: John Wiley & Sons.
Dietz, E. J. (1993), "A Cooperative Learning Activity on Methods of Selecting a Sample," The American Statistician, 47, 104-108.
Eckert, R. E. (1996), "Applied Statistics. Are ChE Educators Meeting the Challenge?," Chemical Engineering Education, Spring 1996, 122-125.
"Evaluation of Undergraduate Statistics Education in Mathematical Statistics" (1995), Utvärdering av grundutbildningen i matematisk statistik vid matematisk-naturvetenskapliga fakulteten i Lund -- Självvärdering (in Swedish), Department of Mathematical Statistics, Lund University.
Gal, I., and L. Ginsburg (1994), "The Role of Beliefs and Attitudes in Learning Statistics: Towards an Assessment Framework," Journal of Statistics Education [Online], 2(2). (http://jse.amstat.org/v2n2/gal.html)
Garfield, J. (1993), "Teaching Statistics Using Small-Group Cooperative Learning," Journal of Statistics Education [Online], 1(1). (http://jse.amstat.org/v1n1/garfield.html)
Garfield, J. (1994), "Beyond Testing and Grading: Using Assessment to Improve Student Learning," Journal of Statistics Education [Online], 2(1). (http://jse.amstat.org/v2n1/garfield.html)
Garfield, J. (1995), "How Students Learn Statistics," International Statistical Review, 63(1), 25-34.
Goedhart, M. J., and A. H. Verdonk (1991), "The Development of Statistical Concepts in a Design-Oriented Laboratory Course in Scientific Measuring," Journal of Chemical Education, 68(12), 1005-1009.
Herdan, G. (1960), Small Particle Statistics, London: Butterworth & Co.
Hogg, R. V. (1985), "Statistical Education for Engineers: An Initial Task Force Report," The American Statistician, 39, 168-175.
Hogg, R. V. (1991), "Statistical Education: Improvements are Badly Needed," The American Statistician, 45, 342-343.
Kopas, D. A., and P. R. McAllister (1992), "Process Improvement Exercises for the Chemical Industry," The American Statistician, 46(1), 34-41.
Lindgren, L., Zetterqvist, L. and G. Holmstedt (1993), "Estimation of Quantiles in Airborne Pollution; Measuring Pollution Around Gas Furnaces," in Statistics for the Environment, eds. V. Barnett and K. F. Turkman, New York: John Wiley & Sons.
Nelson, P., and T. Wallenius (1993), "Improving the Undergraduate Statistical Education of Engineers," supplement to "Reconsidering Statistics Education: A National Science Foundation Conference," by G. Cobb, Journal of Statistics Education [Online], 1(1). (http://jse.amstat.org/v1n1/cobb.supp.nelson.html)
Olbjer, L. (1996), "Experimental and Industrial Statistics" (in Swedish), Department of Mathematical Statistics, Lund University.
Palasota, J. A., and S. N. Deming (1992), "Central Composite Experimental Designs, Applied to Chemical Systems," Journal of Chemical Education, 69(7), 81-85.
Rawlings, J. O. (1988), Applied Regression Analysis: A Research Tool, Pacific Grove, CA: Wadsworth & Brooks/Cole.
Roberts, R. S., M. Johnson, and C. Gorton (1990), "Laboratory Experiments to Reinforce the Use of Statistics in Chemical Engineering," presented at the AIChE Annual Meeting, Chicago, Illinois, November 11-16, 1990.
Romero, R., Ferrer A., Capilla C., Zunica L., Balasch S., Serra V., and Alcover, R. (1995), "Teaching Statistics to Engineers: An Innovative Pedagogical Experience," Journal of Statistics Education [Online], 3(1). (http://jse.amstat.org/v3n1/romero.html)
Smith and Wood (1995), "The Influence of Assessment Strategies on Student Learning in University Mathematics," School of Mathematical Sciences, University of Technology, Sydney.
Vannerberg, C. and G. Holmstedt (1989), "Spridning av NO_2 fran en naturgaseldad villapanna" (in Swedish), Report of Department of Fire Safety Engineering, Lund University, 1-23.
Zetterqvist, L. (1994), Svårighetströsklar i kurserna ``Matematisk statistik for kemister" (Rapport från projektarbete i inspirationskurs vid LTH) (in Swedish), Department of Mathematical Statistics, Lund University.
Zetterqvist, L. (1996), "Working Material in the Course Statistics for Chemistry Students" (in Swedish), Department of Mathematical Statistics, Lund University.
Lena Zetterqvist
Department of Mathematical Statistics
Box 118
S-221 00 Lund
Sweden